Text Solution
Verified by Experts
|
Topper's Solved these Questions
PHYSICAL FUNDAMENTALS OF MECHANICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Elastic Deformation Of Asolid Body|25 VideosView PlaylistPHYSICAL FUNDAMENTALS OF MECHANICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Hydrodynamics|25 VideosView PlaylistPHYSICAL FUNDAMENTALS OF MECHANICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Universal Gravitation|34 VideosView PlaylistOSCILLATIONS AND WAVES
IE IRODOV, LA SENA & SS KROTOV|Exercise Electromagnetic Waves, Radiation|36 VideosView PlaylistTHERMODYNAMICS AND MOLECULAR PHYSICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Transport Phenomena|38 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
IE IRODOV, LA SENA & SS KROTOV-PHYSICAL FUNDAMENTALS OF MECHANICS-Dynamics Of A Solid Body
- A conical pendulum, a thin uniform rod of length l and mass m, rotates...
06:27
|
Play - A uniform cube with edge a rests on a horizontal plane whose friction ...
06:22
|
Play - A smooth uniform rod AB of mass M and length l rotates freely with an ...
11:15
|
Play - A uniform rod of mass m=5.0kg and length l=90cm rests on a smooth hori...
09:20
|
Play - A thin uniform square plate with side l and mass M can rotate freely a...
10:23
|
Play - A vertically oriented uniform rod of mass M and length l can rotate ab...
20:24
|
Play - A horizontally oriented uniform disc of mass M and radius R rotates fr...
08:49
|
Play - A man of mass m1 stands on the edge of a horizontal uniform disc of ma...
08:34
|
Play - Two horizontal discs rotate freely about a vertical axis passing throu...
07:24
|
Play - A small disc and a thin uniform rod of length l, whose mass is eta tim...
15:17
|
Play - A stationary platform P which can rotate freely about a vertical axis ...
16:52
|
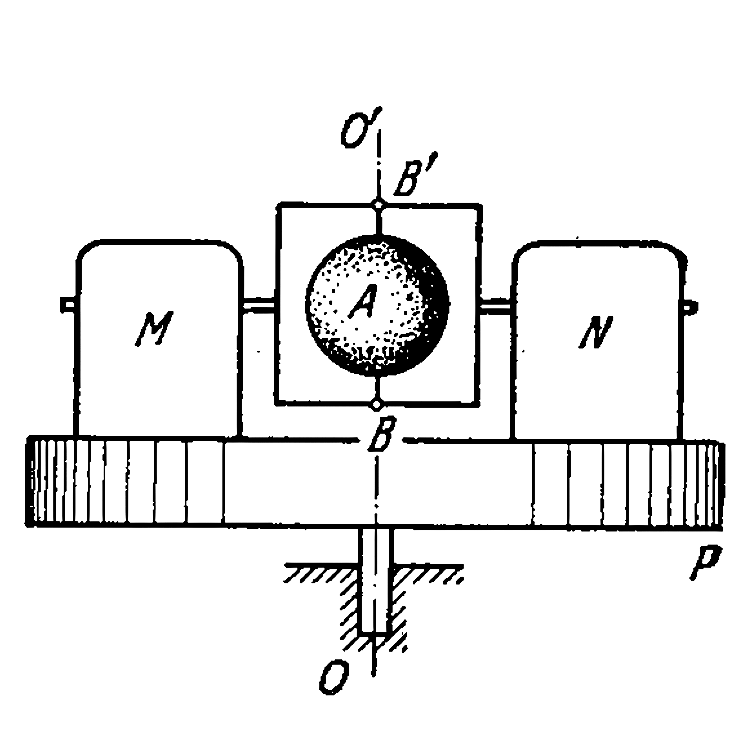
Playing Now - A horizontally oriented uniform rod AB of mass m=1.40kg and length l0=...
09:09
|
Play - The middle of a uniform rod of mass m and length l is rigidly fixed to...
Text Solution
|
Play - A top of mass m=0.50kg, whose axis is tilted by an angle theta=30^@ to...
12:53
|
Play - A gyroscope, a uniform disc of radius R=5.0cm at the end of a rod of l...
Text Solution
|
Play - A top of mass m=1.0kg and moment of inertia relative to its own axis I...
Text Solution
|
Play - A uniform sphere of mass m=5.0kg and radius R=6.0cm rotates with an an...
06:45
|
Play - A cylindrical disc of a gyroscope of mass m=15kg and radius r=5.0cm sp...
Text Solution
|
Play - A ship moves with velocity v=36km per hour along an arc of a circle of...
03:33
|
Play - A locomotive is propelled by a turbine whose axle is parallel to the a...
03:30
|
Play