Home
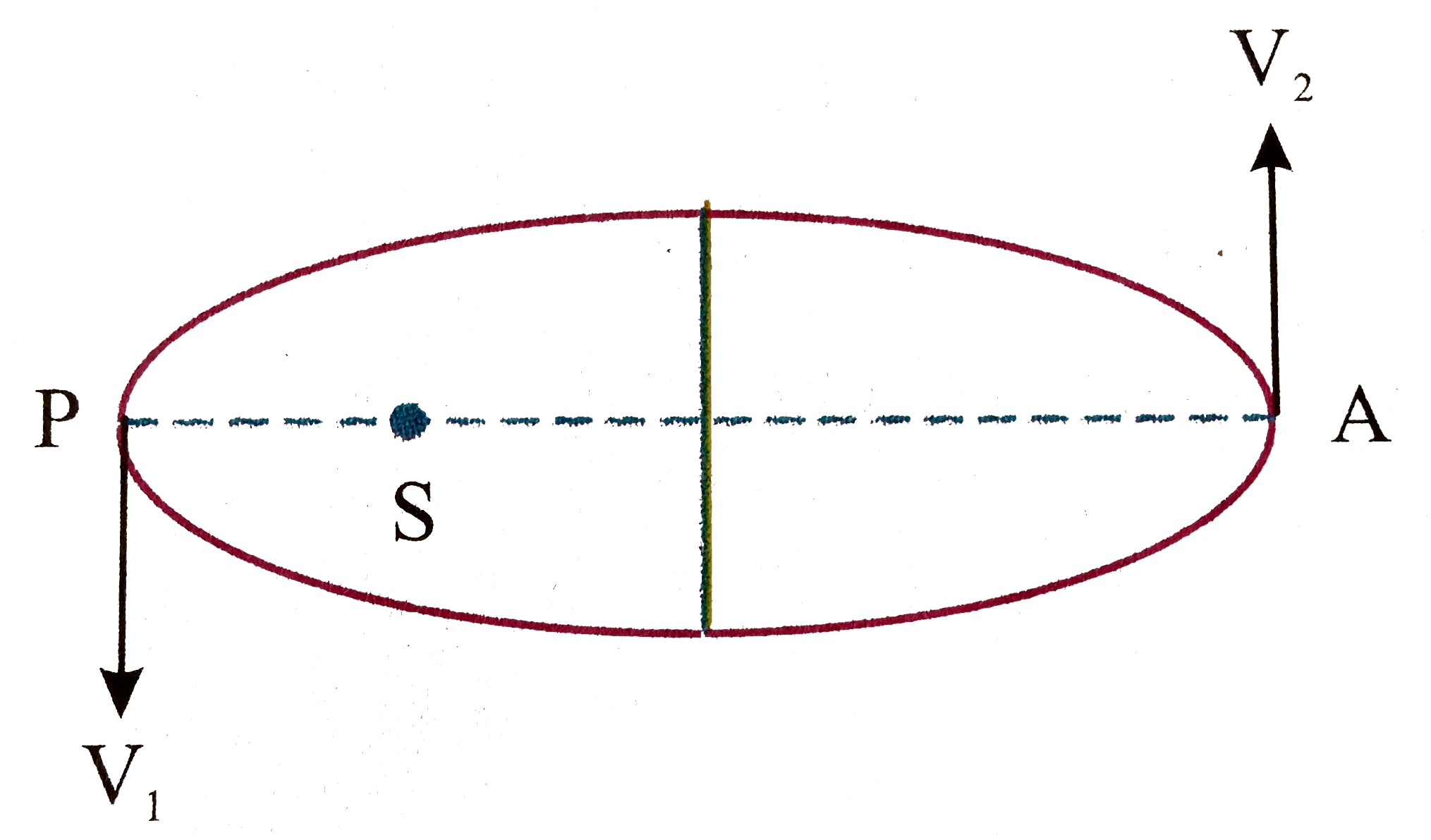
Class 11
PHYSICS
A planet of mass m is moving in an ellip...


A planet of mass `m` is moving in an elliptical orbit around the sun of mass `M`. The semi major axis of its orbit is a, eccentricity is `e`.
Find speed of planet `V_(2)` at aphelion `A`.

A

`sqrt((GM)/a((1+e))/((1-e)))`

B

`sqrt((GM)/a((1-e))/((1+e)))`

C

`sqrt((GM)/(a^(3))((1+e^(2)))/((1-e^(2))))`

D

`sqrt((GM)/(a^(3))((1-e^(2)))/((1+e^(2))))`

Text Solution

Verified by Experts

The correct Answer is:
B
From the given information, `E_(x)=10N//kg`
But, no information is provided about `E_(y)` and `E_(z)` So, `E=sqrt(E_(x)^(2)+E_(y)^(2)+E_(z)^(2))=10N//lg` if `E_(y)=E_(z)=0gt10N//kg` if `E_(y)` and `//` or `E_(z)` are non-zero values
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • GRAVITATION

    NARAYNA|Exercise ILLUSTRATION|49 Videos

  • GRAVITATION

    NARAYNA|Exercise EVALUATE YOURSELF -1|3 Videos

  • GRAVITATION

    NARAYNA|Exercise LEVEL-V|54 Videos

  • FRICTION

    NARAYNA|Exercise Passage type of questions I|6 Videos

  • KINETIC THEORY OF GASES

    NARAYNA|Exercise LEVEL-III(C.W)|52 Videos

Similar Questions

Explore conceptually related problems

Find the speeds of a planet of msdd m in its perihelion and aphelion postitions. The semimajor axis of its orbit is a, ecentricity is e and te mass of the sun is M . Also find the total energy of the planet in terms of the given parameters.

The areal velocity of a planet of mass m moving in elliptical orbit around the sun with an angular momentum of L units is equal to

Knowledge Check

  • A planet of mass m is moving in an elliptical orbit around the sun of mass M . The semi major axis of its orbit is a, eccentricity is e . Find speed of planet V_(1) at perihelion P

    A
    `sqrt((GM)/a((1+e))/((1-e)))`
    B
    `(1+e)/(1-e)sqrt((GM)/a)`
    C
    `sqrt((GM)/(a^(3))((1+e))/((1-e)))`
    D
    `sqrt((GM)/(a^(3))((1+e^(2)))/((1-e^(2))))`

  • A planet of mass m is moving in an elliptical orbit around the sun of mass M . The semi major axis of its orbit is a, eccentricity is e . Find total energy of planet interms of given parameters.

    A
    `-(GMm)/(4a)`
    B
    `-(GMm^(2))/(2a)`
    C
    `-(GMm)/(8a)`
    D
    `-(GMm)/(2a)`

  • A planet of mass m is moving around the sun in an elliptical orbit of semi-major axis a :

    A
    The total mechanical energy of the planet is varying periodically with time
    B
    The total energ of the planet is constant and equals `- (GmM_(s))/(2a), N_(s)` is mass of sun
    C
    Total mechanical energy of the planet is constant and equals `- (GmM_(s))/(a), M_(2)` is mass of sun
    D
    Date is insufficient of arrice at a conclusion

    • Similar Questions

    Explore conceptually related problems

    A hypothetical planet of mass m is moving along an elliptical path around sun of mass M_s under the influence of its gravitational pull. If the major axis is 2R, find the speed of the planet when it is at a distance of R from the sun.

    A planet revolves in an elliptical orbit around the sun. The semi-major and minor axes are a and b , then the time period is given by :

    A planet of mass m is in an elliptical orbit about the sun with an orbital period T . If A be the area of orbit, then its angular momentum would be

    A planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are r_(1) and r_(2) respectively. The period of revolution of the planet wil be proportional to :

    A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at

    Home
    Profile