A particle of mass `M` attached to an inextensible strintg is moving in a vertical circle of radius `R`.about fixed point `O`. It is imparted a velocity `u` in horizontal directional at lowest position as shown in figure.
Following information is being given
(i) Velocity at a height `h` can be calculated by using formula `v^(2)=u^(2)-2gh`
(ii) Particle will complete the circle if `u ge sqrt(5gR)`
(iii) Particle will oscillates in lower half `(0^(@)ltthetale90^(@))` if `0ltu lesqrt(2gR)`
(iv) The magnitude of tension at a height `'h'` is calculated by using formula `T=M/R[u^(2)+[gR-3gh]]`
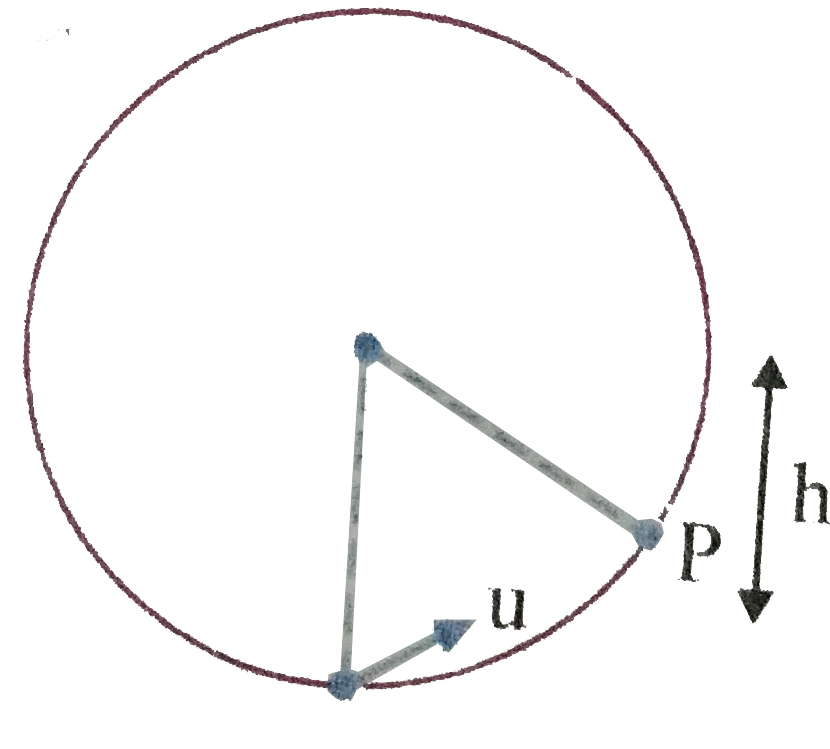
If `R = 2m, M = 2 kg` and `u = 12 m//s`. Then value of tension at lowest position is