A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
WORK POWER AND ENERGY
NARAYNA|Exercise Level-VI (Comprehension)|20 VideosView PlaylistWORK POWER AND ENERGY
NARAYNA|Exercise Level-VI (Integer)|12 VideosView PlaylistWORK POWER AND ENERGY
NARAYNA|Exercise Level-VI (Single Answer)|31 VideosView PlaylistWORK , ENERGY & POWER
NARAYNA|Exercise EXERCISE IV|43 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
NARAYNA-WORK POWER AND ENERGY-Level-VI (Multiple Answer)
- The potential energy of a particle moving along x-axis is given by U =...
02:44
|
Play - A block of mass 1 kg moves towards a spring of force constant 10 N//m....
04:01
|
Play - The spring constant of spring A is twice the spring constant of spring...
03:25
|
Play - A particle of mass 1 kg is moving X-axis. Its velocity is 6 m//s at x ...
05:00
|
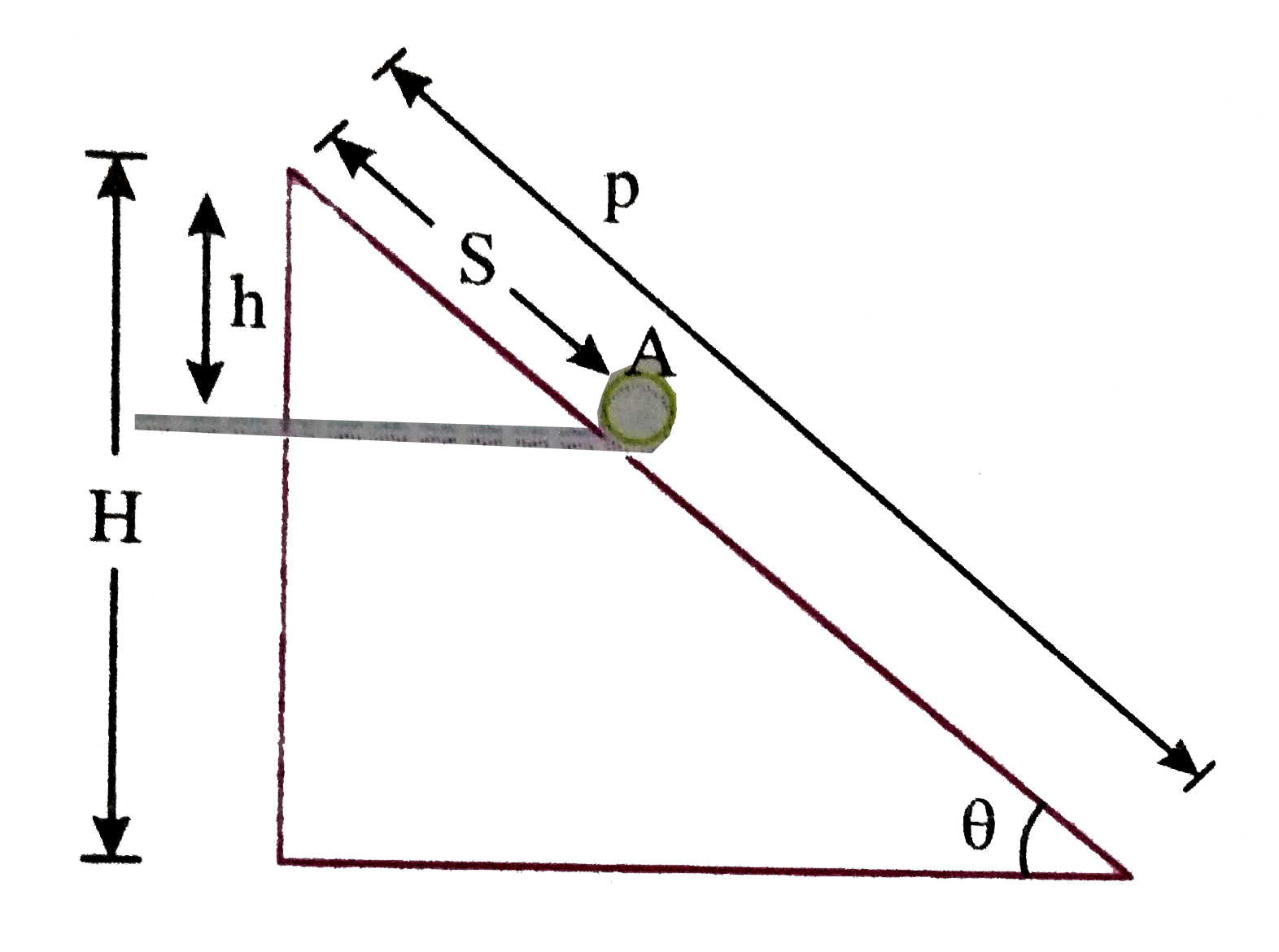
Play - A particle sides down from rest on an inclined plane of angle theta wi...
03:06
|
Playing Now - A particle is taken from point A to point B under the influence of a f...
02:20
|
Play - An engine is pulling a train of mass m on a level track at a uniform s...
02:33
|
Play - The alternative that gives the conservative force of the following is.
03:02
|
Play - A man is standing on a plank which is placed on smooth horizontal surf...
02:37
|
Play - A small sphere of mass m suspended by a thread is first taken a side s...
07:14
|
Play - A particle P is initially at rest on the top pfa smooth hemispherical ...
06:32
|
Play
 .
.