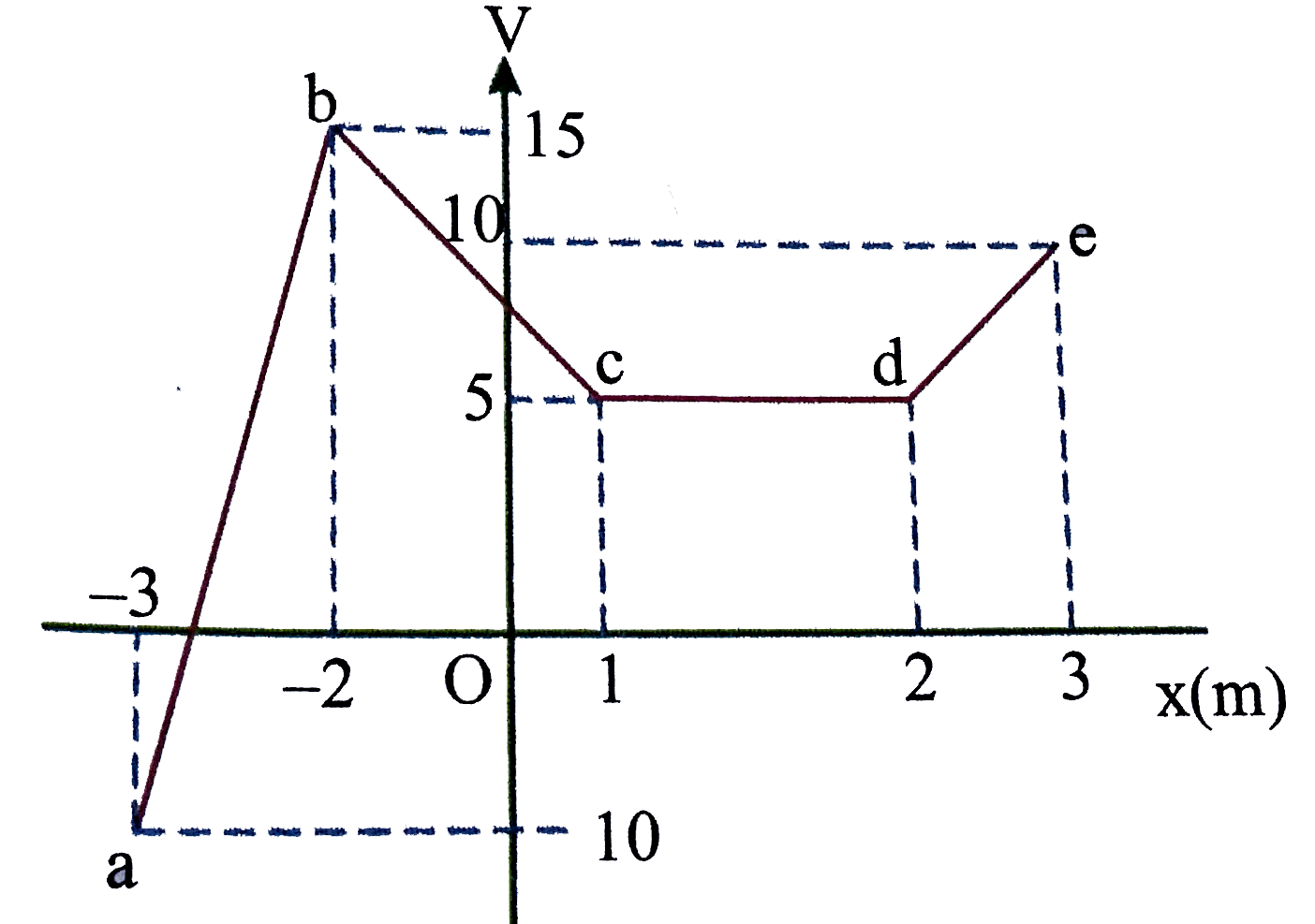
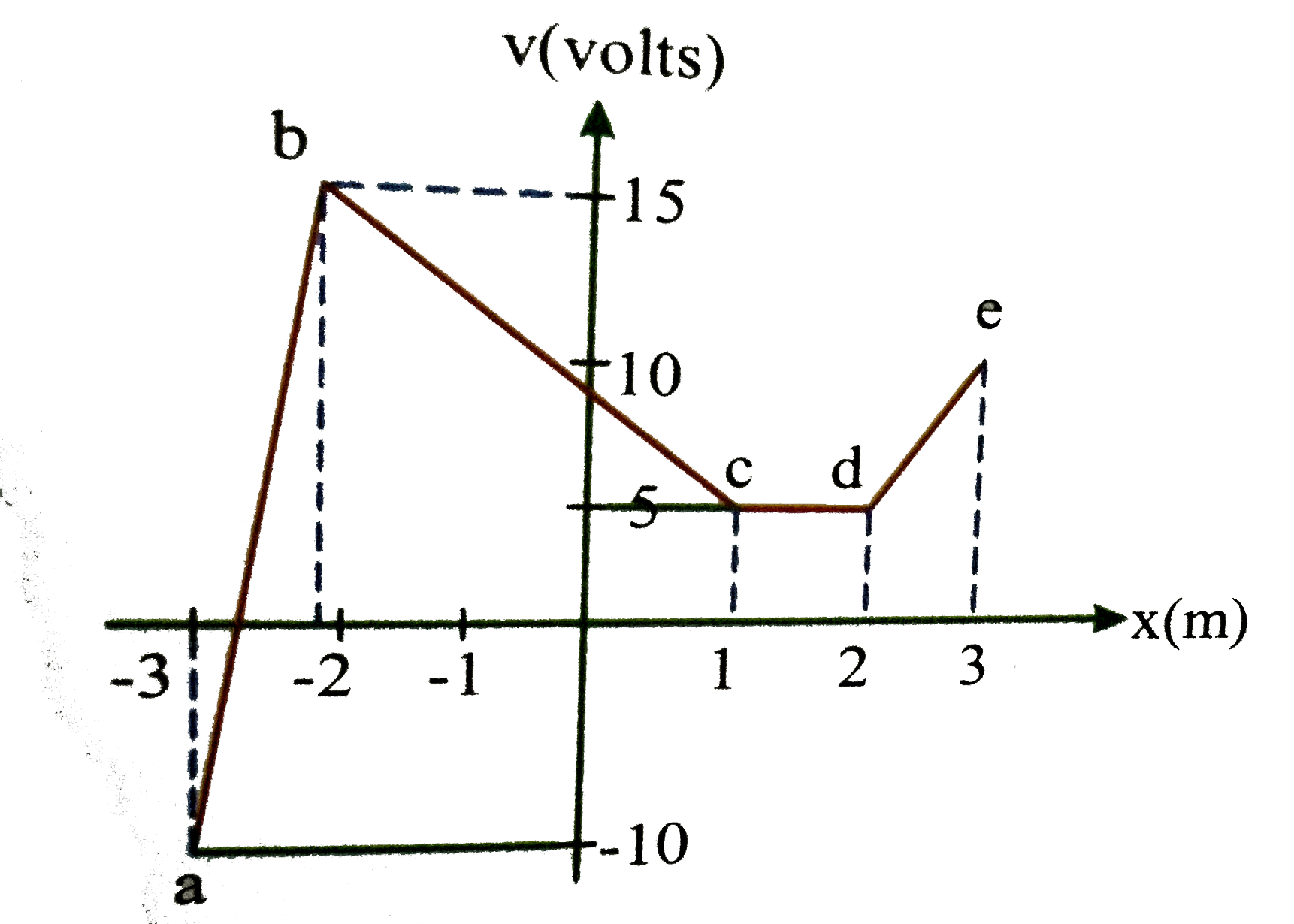Suppose electric potential varies along the x-axis as shown in the above figure the potential doesnot vary in `y or z` direction of the intervals shown (ignore the behaviour at the end points of the intervals) the field `E_(x)` has a maximum absolute value `"FB_(1)"Vm^(-1)` in the region `"FB_(2)"` its value in the region cd is `"FB_(3)"Vm^(-1)` then
The value that fills `"FB_(1)"` is

Options

A. `(25)/(2)`
B. `25`
C. `(15)/(2)`
D. `-50`

Answer

B

Explanation

`(E_(x))_(max)`Value `'FB_(1)'` in the region `FB_(2)`
`E_(x)=value of cd is `FB_(3)Vm^(-1)`
`E=-(dV)/(dx)rArr E_(ab)=-((25)/(1))=-25`
`E_(be)=((5-15)/(1+2))=(10)/(3)E_(cd)=0`
`E_(de)=-((15-5)/(3-2))=-10`
`rArr (E_(x))_(Max)=25V//m^(-1)rArr FB_(2)` is ab
Taking the values of `E_(ab),E_(bc),E_(cd),E_(de)` .The plot of `E_(x)` Vsx will be as shown in `D` option.
For `a rarr b` part `V =25x+65`
`:.when `V=0rArr x=(-65)/(25)=(-13)/(5)m`