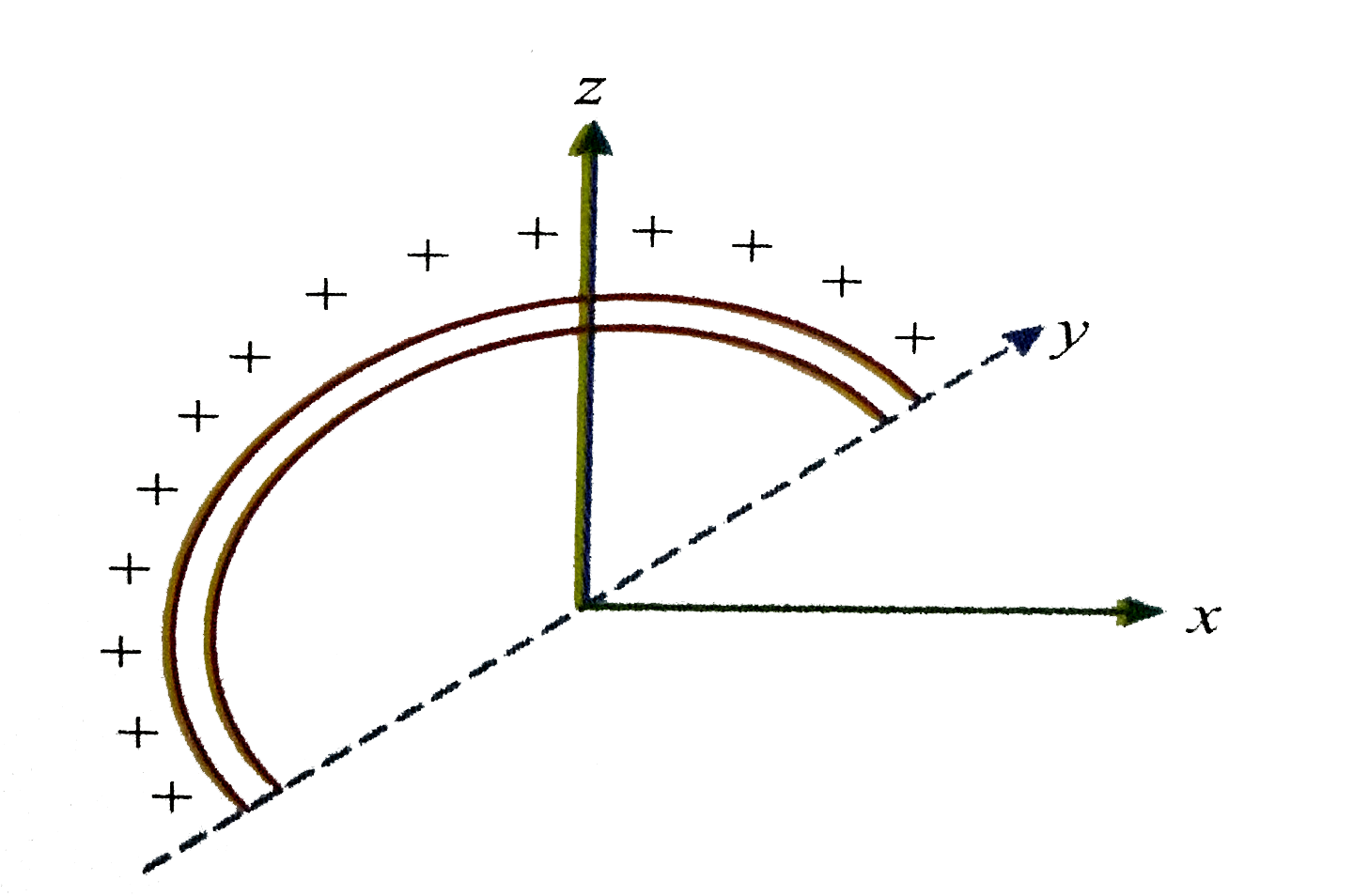
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ELECTROSTATICS AND GAUSS LAW
NARAYNA|Exercise Passage IV|5 VideosELECTROSTATICS AND GAUSS LAW
NARAYNA|Exercise Passage V|3 VideosELECTROSTATICS AND GAUSS LAW
NARAYNA|Exercise Passage II|3 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
NARAYNA|Exercise ADDITIONAL PROBLEMS|14 VideosEXPERIMENTAL PHYSICS
NARAYNA|Exercise Comprehension type|6 Videos
Similar Questions
Explore conceptually related problems