Home
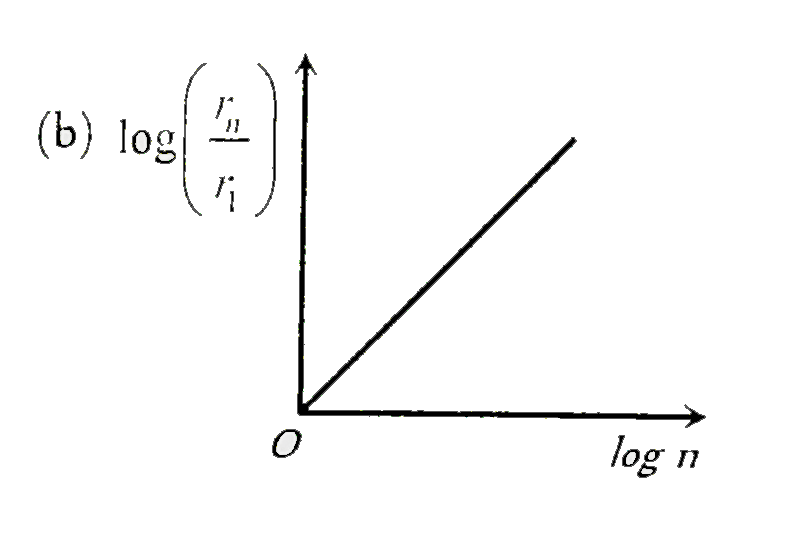
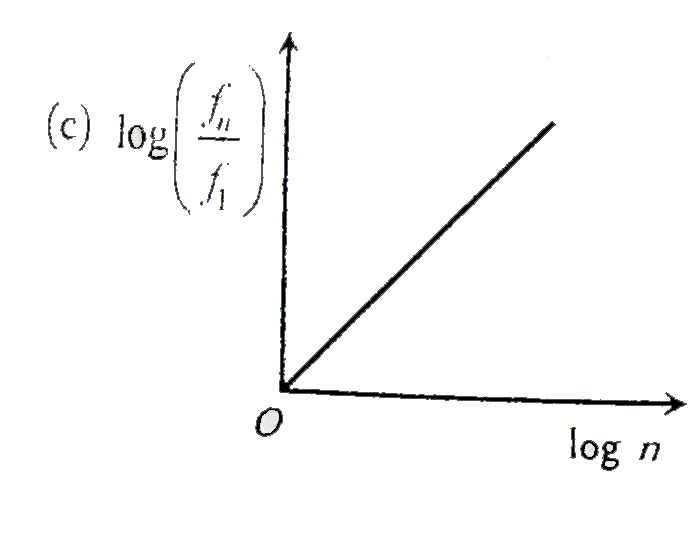Class 12
PHYSICS
Frequency of revolution of electron in t...

Frequency of revolution of electron in the `n^(th)` Bohr's orbit is given by

A

`f=(me^(4))/(4 in_(0)^(2)n^(3)h^(3))`

B

`f=4 in_(0)^(2)n^(3)h^(3)`

C

`f=(me^(4))/(4 in_(0)^(2)h^(2))`

D

`f=(me^(4))/(in_(0) n)`

Text Solution

Verified by Experts

The correct Answer is:
A
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • CIRCULAR MOTION

    NIKITA PUBLICATION|Exercise Multiple Choice Question|421 Videos

Similar Questions

Explore conceptually related problems

The frequency of revolution of electron in n^("th") Bohr orbit is v_(n) .The graph between log n and log(v_(n)/v_(1)) may be

Obtain an expression for the frequency of revolution of the electron in the nth Bohr orbit.

Knowledge Check

  • Period of revolution of electron in the n^(th) bohr's orbit is given by

    A
    `T =(4 in_(0)^(2) n^(3) h^(3))/(me^(4))`
    B
    `T=4 in_(0)^(2) n^(3) h^(3)`
    C
    `T=me^(4) n`
    D
    `T=2pi`

  • According to Bohr's theory frequency of the revolution of electron in a Bohr's orbit is inversely proportional to

    A
    principle quantum number
    B
    square of principle quantum number
    C
    cube of principle quantum number
    D
    forth power of principle quantum number

  • If in hydrogen atom, radius of n^(th) Bohr orbit is , n_(r) frequency of revolution of electron in n^(th) orbit is f_(n) choose the correct option

    A
    B
    C
    D
    Both (a) and (b)

    • Similar Questions

    Explore conceptually related problems

    The frequency of revolutions of the electron in the first Bohr orbit in the hydrogen atom is 6.576 xx 10^(15) Hz. What is the frequency of revolution in the second Bohr orbit?

    Calculate the frequency of revolution of electron in the first Bohr orbit of hydrogen atom, if radius of first Bohr orbit is 0.5Å and velocity of electron in the first orbit is 2.24xx10^6m//s .

    Calculate the frequency of revolution of electron in the second Bohr's orbit of radius 2.12Å. Given, h=6.6xx10^(-34)Js, m=9xx10^(-31)kg .

    Calculate the frequency of revolution of the electron in this second Bohr orbit of the hydrogen atom. The radius of the orbit is 2.14 Å and the speed of the electron in the orbit is 1.09 xx 10^(6) m//s .

    Calculate the angular frequency of revolution of an electron occupying the second Bohr orbit of He^(+) ion.

    Home
    Profile