Home
Class 9
MATHS
A B is a line segment. P\ a n d\ Q are p...

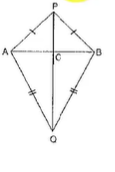
`A B` is a line segment. `P\ a n d\ Q` are points on opposite sides of `A B` such that each of them is equidistant from the points `A\ a n d\ B` (in figure). Show that the line `P Q` is perpendicular bisector of `A B`

Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    RD SHARMA|Exercise All Questions|306 Videos

  • CONSTRUCTION

    RD SHARMA|Exercise All Questions|29 Videos

Similar Questions

Explore conceptually related problems

AB is a line-segment.P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig.7.37 ).Show that the line PQ is the perpendicular bisector of AB

In the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.

AB is a line segment and line l is its perpendicular bisector.If a point P lies on l show that P is equidistant from A and B.

AB is a line segment and line 1 is its perpendicular bisector.If a point P lies on 1 show that P is equidistant from A and B .

If the point P(p,q) is equidistant from the points A(a+b,b-a)and B(a-b,a+b), then

Show that the locus of a point, equidistant from the endpoints of a line segment, is the perpendicular bisector of the segment

If a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.

A B is a line segment, A X and B Y are two equal line segments drawn on opposite sides of line A B such that A X B Ydot If A B and X Y intersect each other P , prove that A P X~=B P Y A B and X Y bisect each other.

In figure P is a point equidistant from the lines l and m intersecting at point A. Show that the line n (along AP) bisects the angle between l and m.

RD SHARMA-CONGRUENT TRIANGLE -All Questions
  1. Determine the measure of each of the equal angles of a right-angled ...

    Text Solution

    |

  2. A B C is a right-angled triangle is which /A=90^0a n d\ A B=A Cdot F...

    Text Solution

    |

  3. A B is a line segment. P\ a n d\ Q are points on opposite sides of A...

    Text Solution

    |

  4. In Figure, diagonal A C of a quadrilateral A B C D bisects the angles ...

    Text Solution

    |

  5. A B is a line segment. A X\ a n d\ B Y are two equal line segments d...

    Text Solution

    |

  6. l\ a n d\ m are two parallel lines intersected by another pair of pa...

    Text Solution

    |

  7. In Figure, if A B||D C\ a n d\ P is the mid-point B D , prove that P i...

    Text Solution

    |

  8. In Figure, /B C D=/A D C\ a n d\ /A C B=/B D Adot Prove that A D=B C\ ...

    Text Solution

    |

  9. In two right triangles, one side and an acute angle of one triangle ...

    Text Solution

    |

  10. In Figure, A C=B C ,\ /D C A=/E C B\ a n d\ /D B C=E A Cdot Prove that...

    Text Solution

    |

  11. In Figure, it is given that R T=T S ,\ /1=2/2\ a n d\ /4=2/3 . Prove...

    Text Solution

    |

  12. Two lines A B\ a n d\ C D intersect at O such that B C is equal and pa...

    Text Solution

    |

  13. B D\ a n d\ C E are bisectors of /B\ a n d\ /C of an isosceles A B C ...

    Text Solution

    |

  14. In Figure, A B=A C\ a n d\ D B=D Cdot\ Prove that /A B D=/A C D

    Text Solution

    |

  15. \ a b c is an isosceles triangle with A B=A Cdot Side B Ais produced...

    Text Solution

    |

  16. In Figure, A B=A CdotB E\ a n d\ C F are respectively the bisectors ...

    Text Solution

    |

  17. If A B C is an isosceles triangle with A B=A Cdot Prove that the ...

    Text Solution

    |

  18. If the altitudes from two vertices of a triangle to the opposite sid...

    Text Solution

    |

  19. In Figure, it is given that /A=/C\ a n d\ A B=B Cdot Prove that A B...

    Text Solution

    |

  20. A D\ a n d\ B C are equal perpendiculars to a line segment A B . Sho...

    Text Solution

    |