Home
Class 11
PHYSICS
A particle is dropped from a finite heig...

A particle is dropped from a finite height `H` above the ground level under gravity . Due to air resistance acceleration of particle becomes `a=g-kv` in the direction of velocity. Where `k=` positive constant `&v=` speed of particle. Then which of the following graph`(s)` is `//` are possible `(t_(0)=` time when particle touches the ground `):`

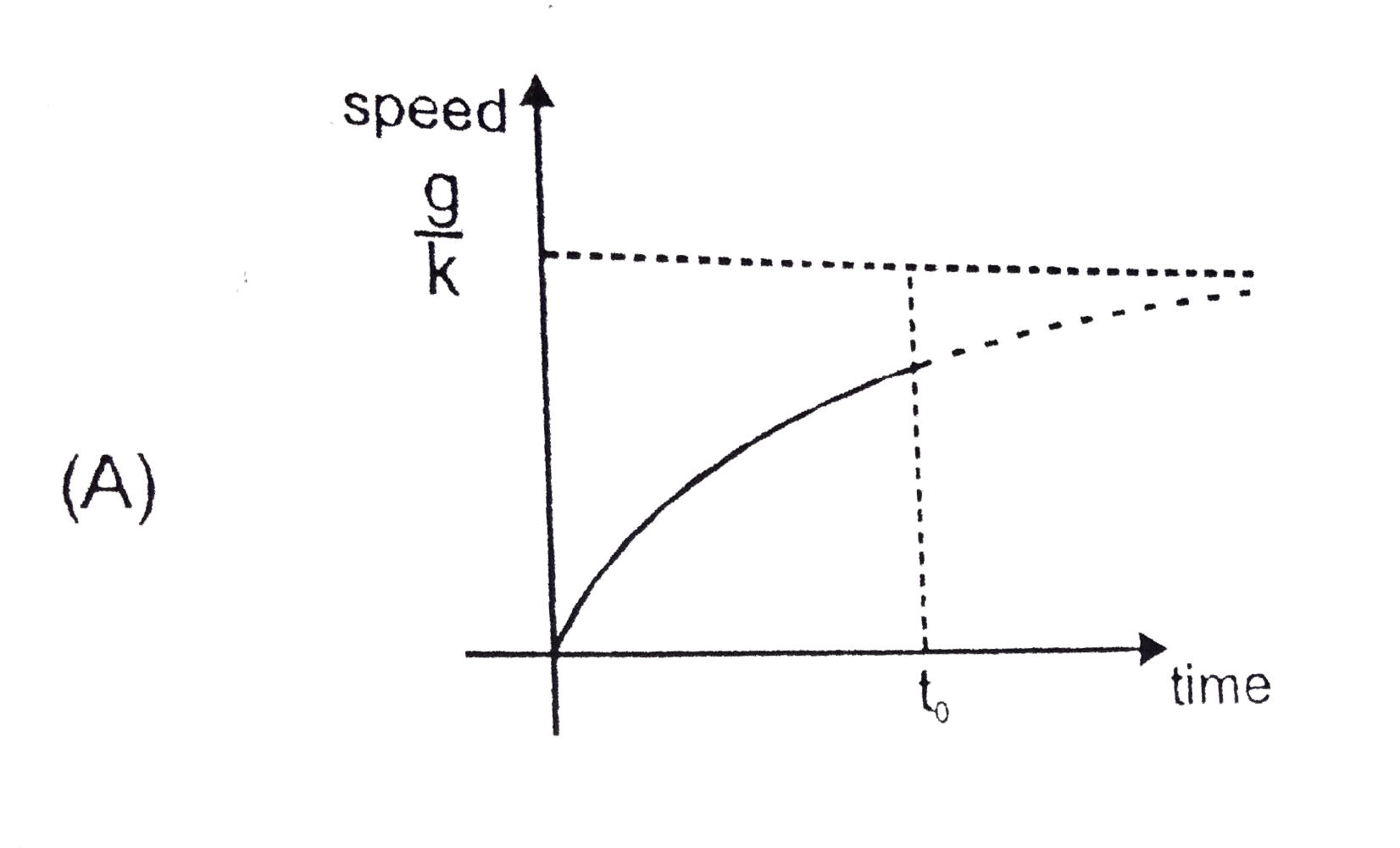
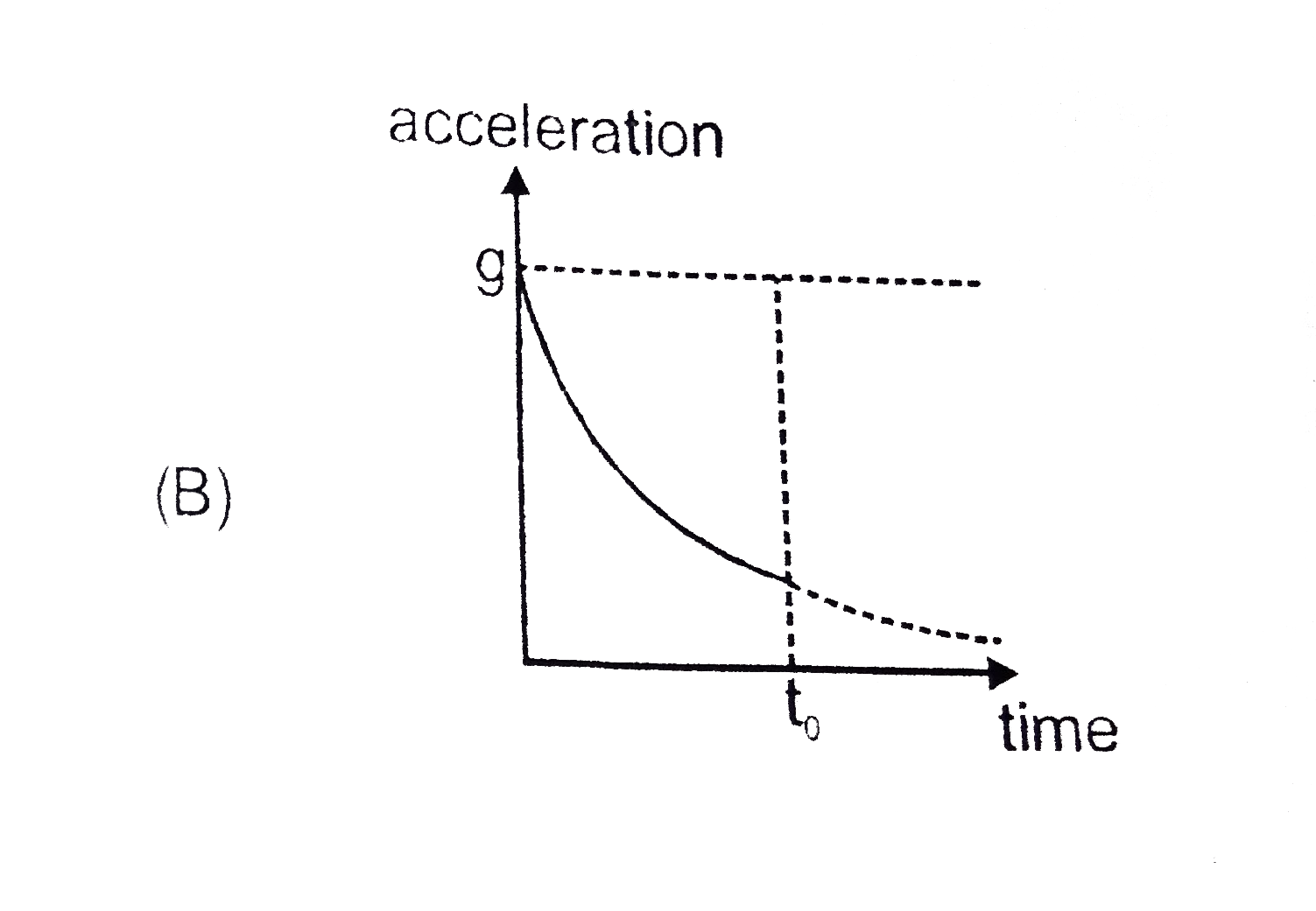
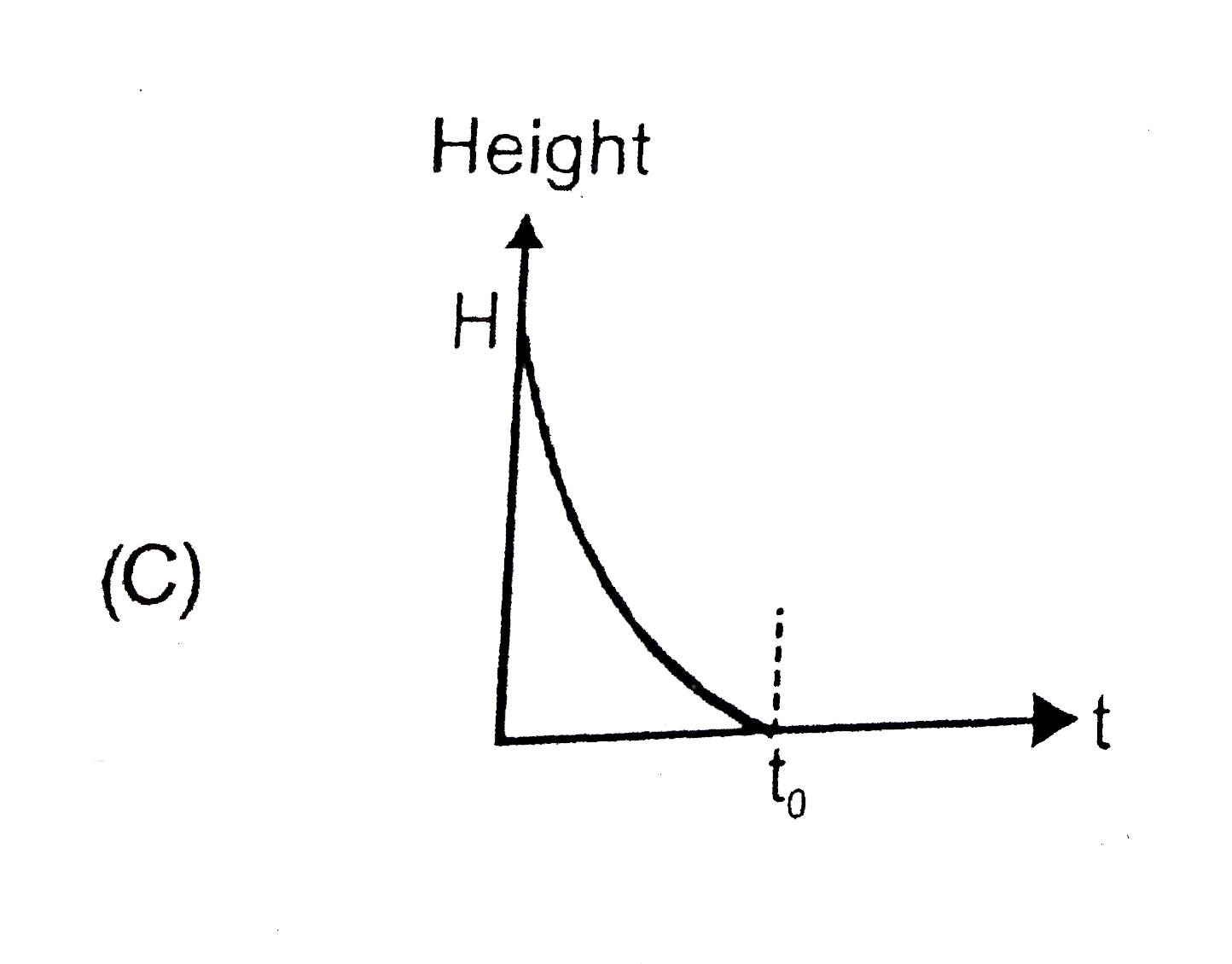
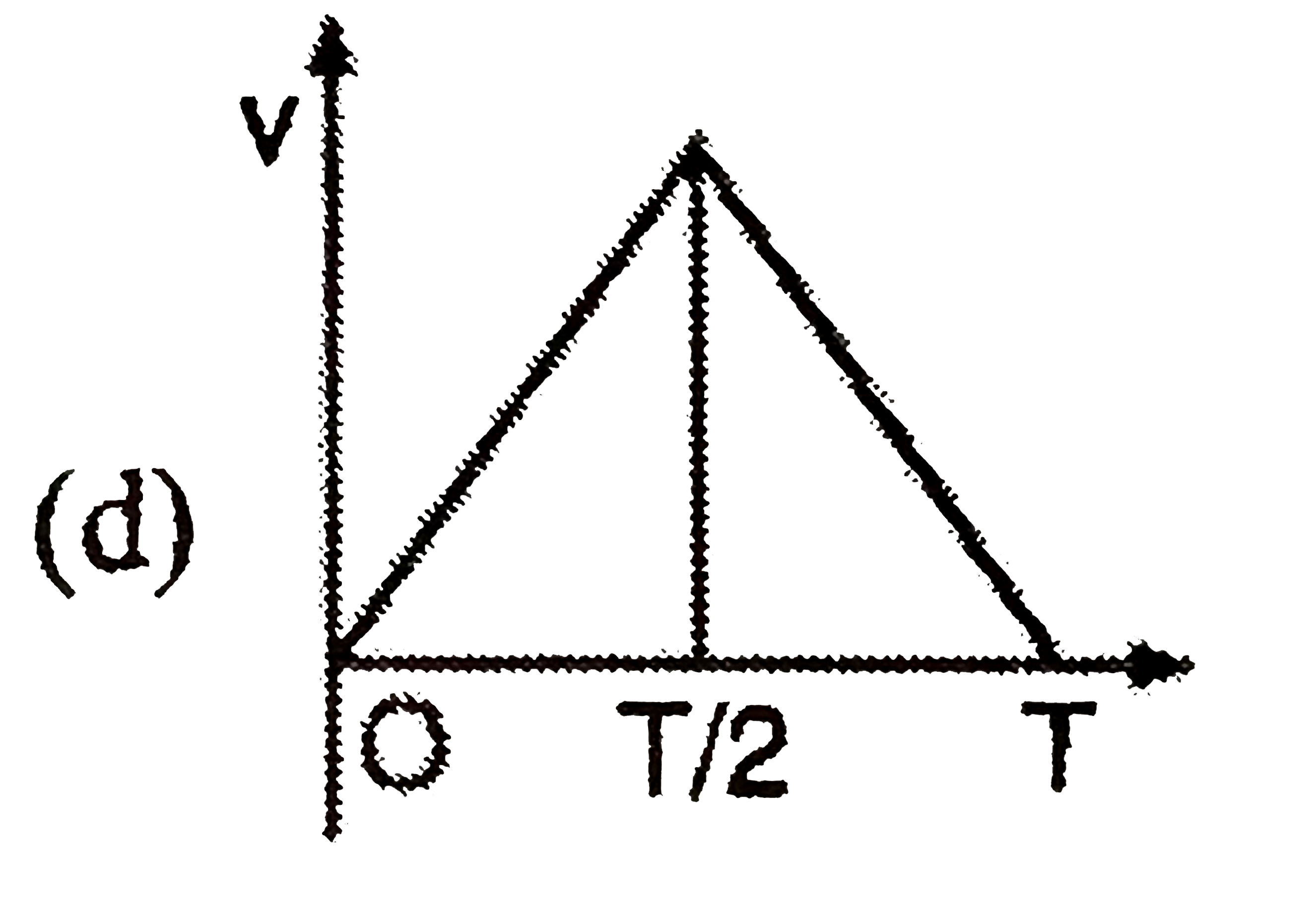
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
A, B, D
`(dv)/(dt)=g-kvunderset(0)overset(v)int(dv)/(g-kv)=underset(t=0)overset(t)int dt`
`-(1)/(-kv)ln((g-kv)/(g))=t`
`g-kv=ge^(-kt)v=(g)/(k)[1-e^(-kt)]`
`a=(g)/(k)[0-e^(-kt)(-k)]`
`=g e^(-kt)`
`V=(g)/(k)-(a)/(k)=-(a)/(k)+(a)/(k)`
`V-(g)/(k)=-(a)/(k)`
`kv-g=-a`
`a=g-kv`
`=-kv+g`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 15|8 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 16 physics|8 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise Dpp no. 13 physics|5 Videos

  • CURRENT ELECTRICITY

    RESONANCE|Exercise Exercise|54 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

Particle is dropped form the height of 20m form horizontal ground. There is wind blowing due to which horizontal acceleration of the particles becomes 6 ms^(-2) . Find the horizontal displacement of the particle till it reaches ground.

A particle is thrown vertically upwards with a velocity v . It returns to the ground in time T. which of the following graphs correctly represents the motion ?

A particle thrown up vertically reaches its highest point in time t_(1) and returns to the ground in further time t_(2) . The air resistance exerts a constant force on the particle opposite to its direction of motion

A particle is dropped from the top of a tower of height 80 m . Find the time of jurney and the speed with which it strikes the ground.

A particle starts from rest and moves with acceleration a which varies with time t as a=kt where k is a costant. The displacement s of the particle at time t is

The velocity of a particle moving in the positive direction of the X-axis varies as V=Ksqrt(S) where K is a positive constant. Draw V-t graph.

A particle is projected vertically upwards with a velocity v. It returns to the ground in time T. Which of the following graphs correctly represents the motion.

The acceleration of a particle travelling along a straight line is a =(k)/(v) , where k is constant (k gt 0) . If at t=0,V=V_(0) then speed of particle at t = (V_(0)^(2))/(2) .

A particle located at position x=0, at time t=0, starts moving along the positive x-direction with a velocity v^2=alpha x (where alpha is a positive constant). The displacement of particle is proportional to

A particle is projected with speed 100m/s at angle theta=60^(@) with the horizontal at time t=0" . At time 't' the velocity vector of the particle becomes perpendicular to the direction of velocity of projection.Its tangential acceleration at time 't' is (g =10m/s^(2))