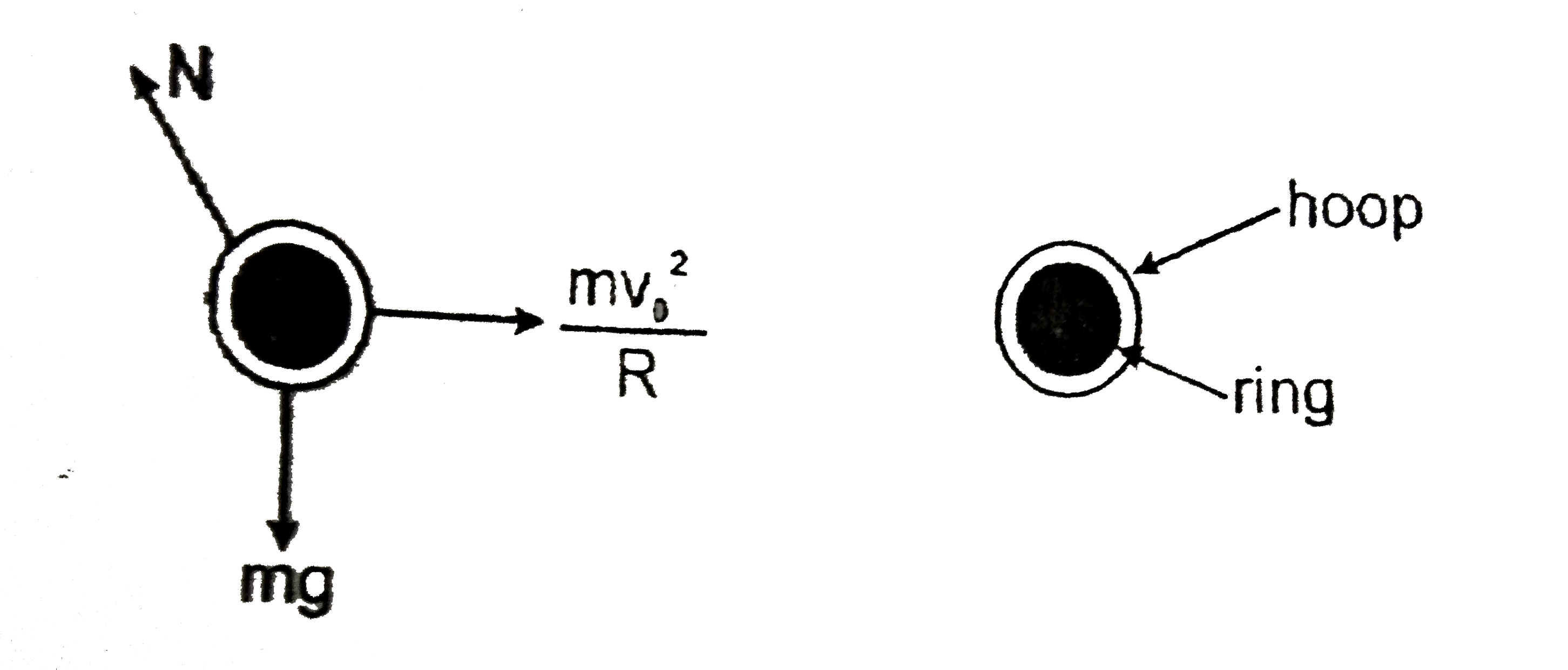A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 52|7 VideosView PlaylistDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 53|5 VideosView PlaylistDAILY PRACTICE PROBLEMS
RESONANCE|Exercise DPP 50|5 VideosView PlaylistCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosView PlaylistELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp 51
- A particle is attached with a string of length l which is fixed at poi...
04:26
|
Play - When a block is placed on a wedge as shown in figure, the block starts...
03:20
|
Play - A shell of mass 4kg moving with a velocoity 10m//s vertically upward e...
04:13
|
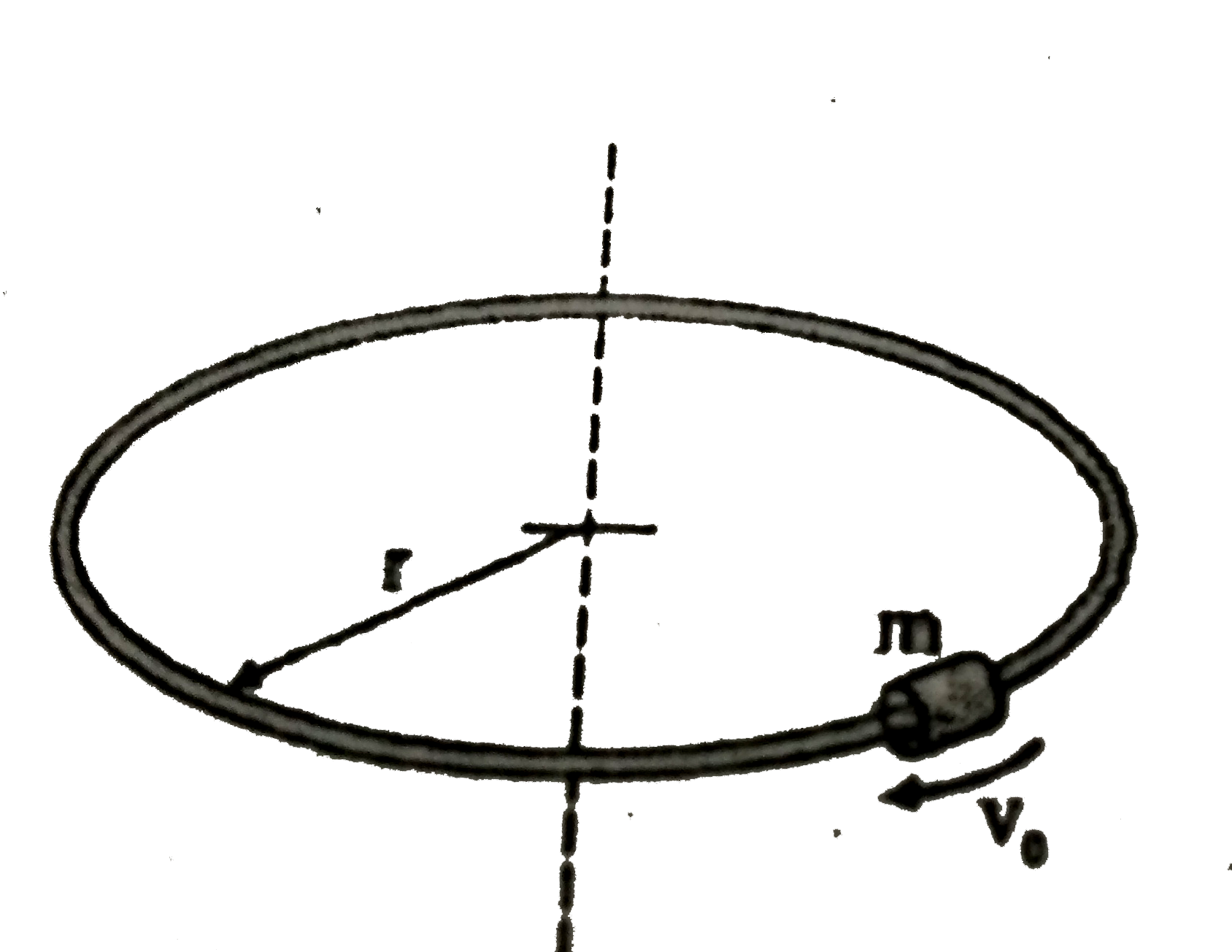
Play - A small hoop of mass m is given an initial velocity of magnitude v(0) ...
02:52
|
Playing Now - A car moves around a curve at a constant speed. When the car goes arou...
03:27
|
Play - Two blocks Aand B ,each of same mass are attached by a thin inextensib...
02:38
|
Play - Mass 2m is kept on a smooth circular track of mass m which is kept on ...
04:15
|
Play