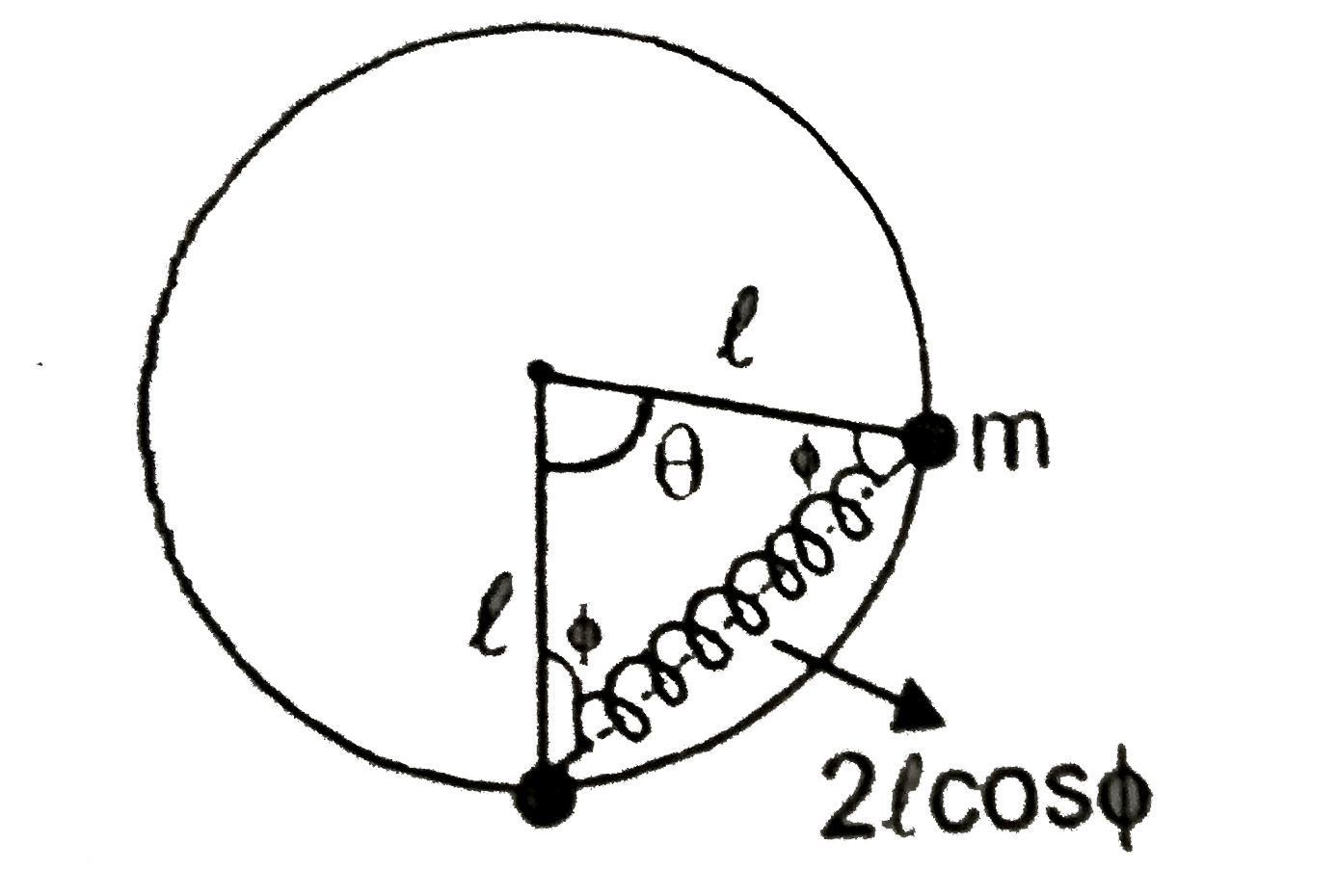
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 51|7 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 52|7 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 49|6 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-DPP 50
- The string is now replaced by a spring of spring constant k and natura...
Text Solution
|
- In the figure PQRS is a frictionless horizontal plane on which a parti...
Text Solution
|
- Two balls of same mass are released simultaneously from heights h & 2h...
Text Solution
|
- Displacement - time curve of a particle moving along a straigh line is...
Text Solution
|
- A particle A of mass m is situated at highest point of wedge B of mass...
Text Solution
|