A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.51|20 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.52|9 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.49|20 VideosCURRENT ELECTRICITY
RESONANCE|Exercise High Level Problems (HIP)|21 VideosELECTRO MAGNETIC WAVES
RESONANCE|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEM-DPP No.50
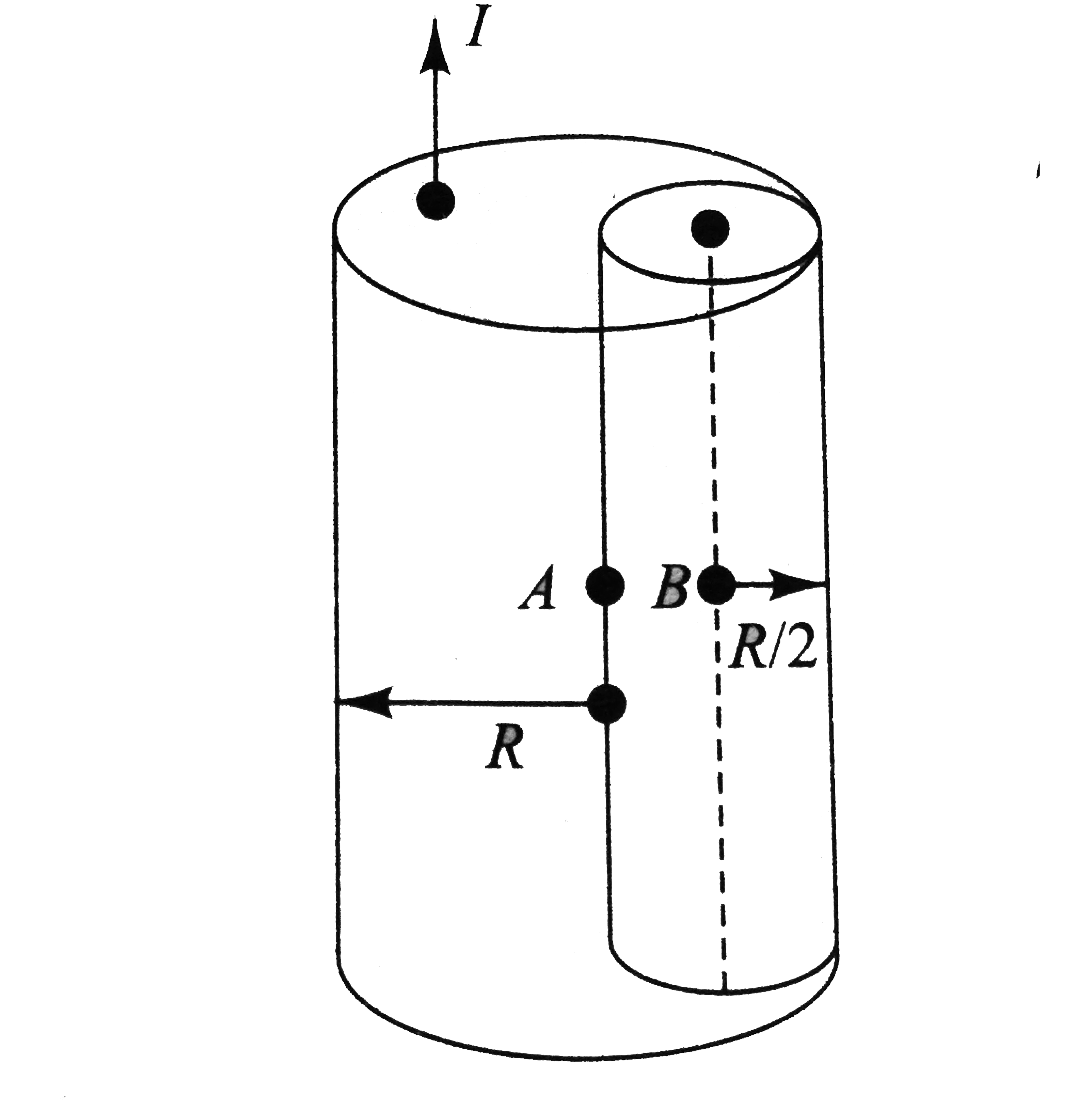
- From a cylinder of radius R, a cylider of radius R//2 is removed, as s...
Text Solution
|
- A block is attached with an ideal spring and string, and is in equilib...
Text Solution
|
- The mean life time of a radionuclide, if the activity decrease by 4% ...
Text Solution
|
- Find the force per unit area on the surface of a long hollow cylinder ...
Text Solution
|
- Figure shows a cubical block of side 10 cm and relative density 1.5 su...
Text Solution
|
- A sphere P (emissivity=1) of radius 2R and and another sphere Q(emissi...
Text Solution
|
- In the circuit arrangement shown in figure capacitor is initially unch...
Text Solution
|
- In the circuit arrangement shown in figure capacitor is initially unch...
Text Solution
|
- In the circuit arrangement shown in figure capacitor is initially unch...
Text Solution
|