Text Solution
Verified by Experts
|
Topper's Solved these Questions
VECTORS
NARAYNA|Exercise C.U.Q|34 VideosView PlaylistVECTORS
NARAYNA|Exercise LEVEL-I (C.W)|27 VideosView PlaylistUNITS AND MEASUREMENTS
NARAYNA|Exercise STATEMENT TYPE QUESTION|23 VideosView PlaylistWAVES
NARAYNA|Exercise Exercise-IV|56 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
NARAYNA-VECTORS-LEVEL-II (H.W)
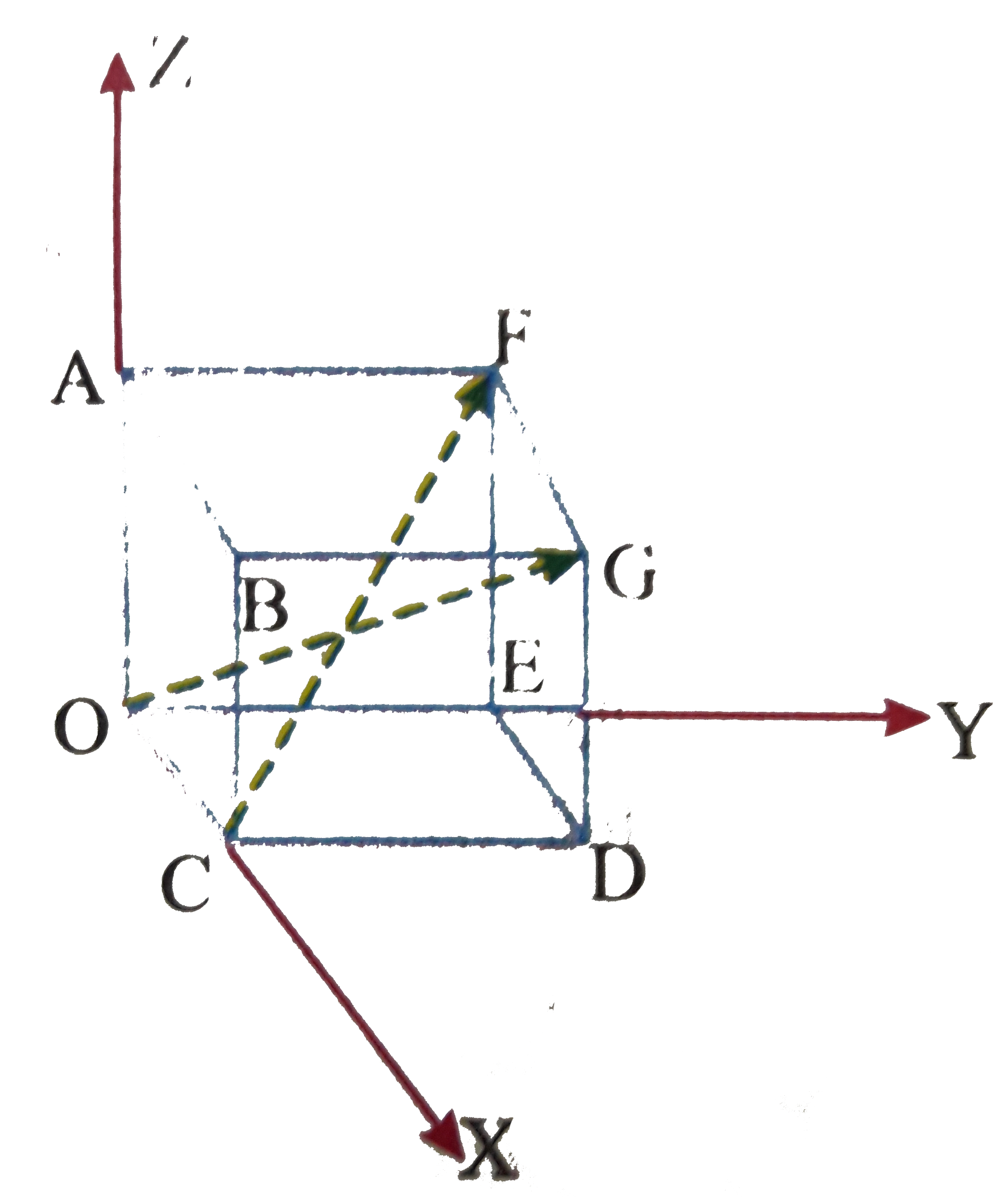
- Find the angle between the diagonals of a cube with edges of length "a...
06:20
|
Playing Now - A particle has a displacement of 12 m towards east then 5 m forwards n...
02:14
|
Play - Four co-planar concurrent forces are acting on a body as shown in the ...
04:23
|
Play - O is apoint on the gournd chosen as origin. A boby first suffers a dis...
04:37
|
Play - If the two directional cosiness of a vectors are (1)/sqrt(2) and (1)/s...
01:53
|
Play - A force vecF=3hati+chatj+2hatkN acting on a particle causes a displace...
02:19
|
Play - If veca and vecb are two unit vectors such that veca+2vecb and 5veca-4...
02:45
|
Play - If vecA=9hati-7hatj+5hatk and vecB=3hati-2hatj-6hatk then the value of...
03:51
|
Play - The work done by a force 2hati-hatj+5hatk when it displaces the body f...
Text Solution
|
Play - The component of vecA along vecB is sqrt(3) times that of the componen...
02:15
|
Play - If vecA=(2hati+3hatj) and vecB=(hati-hatj) then component of vecA perp...
05:56
|
Play - If vecA+vecB=vecR and 2vecA+vecB is perpendicular to vecB then
02:47
|
Play - If vecA=(1)/sqrt(2)cos theta hati+(1)/sqrt(2)sin thetahatj, what will ...
05:44
|
Play - (hati+hatj)xx(hati-hatj)=
02:54
|
Play - The diagonals of a parallelogram are vecA=2hati-3hatj+hatk and vecB=-2...
04:17
|
Play