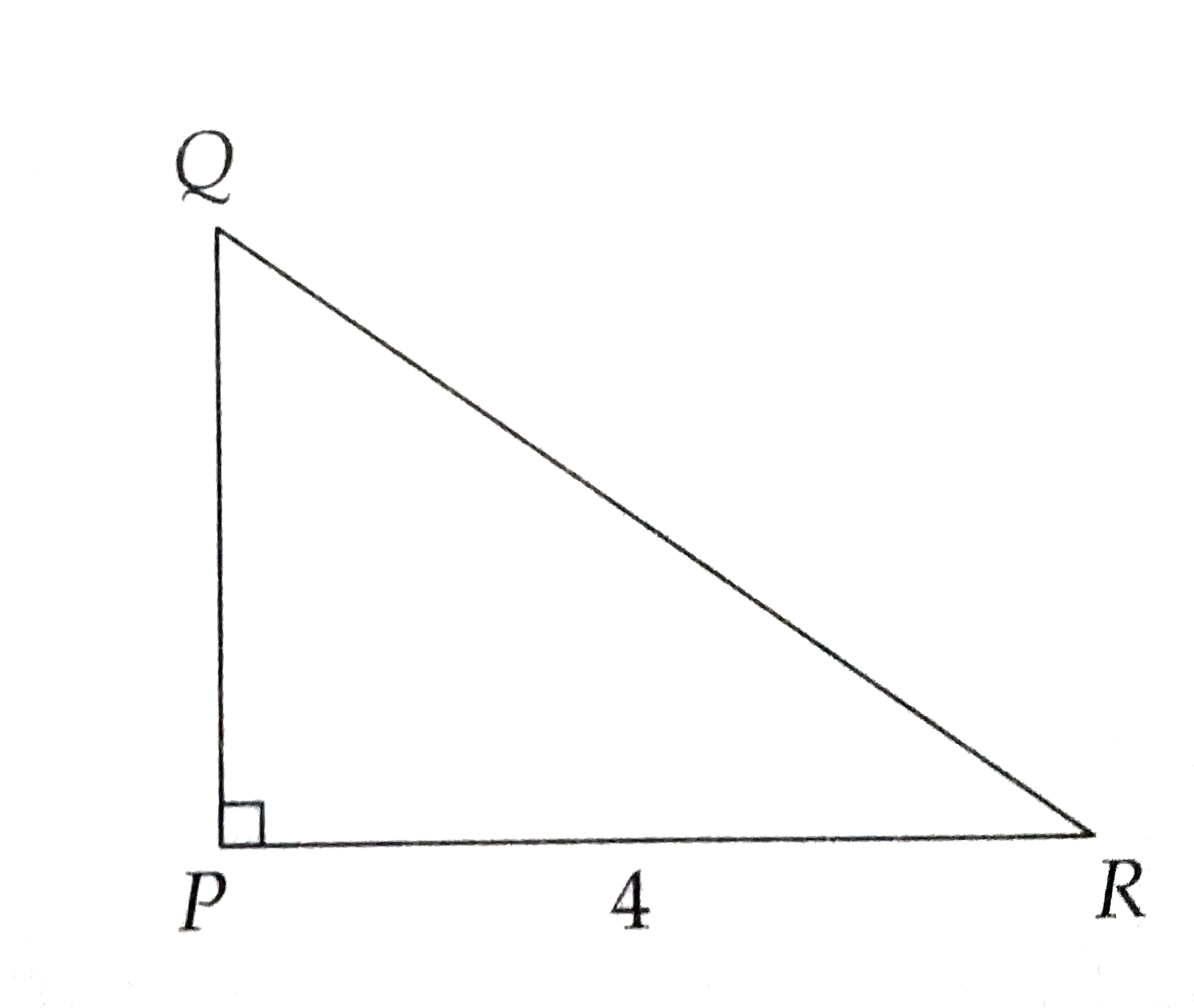
Think about what shape the top and bottom will create when each is rotated about its midpoint.
Can you visualize what the resulting solid looks like ? It can be a little difficult to sketch 3-D geometry. You're probably better off if you can just ''see'' it in your head. It'll look something like this :
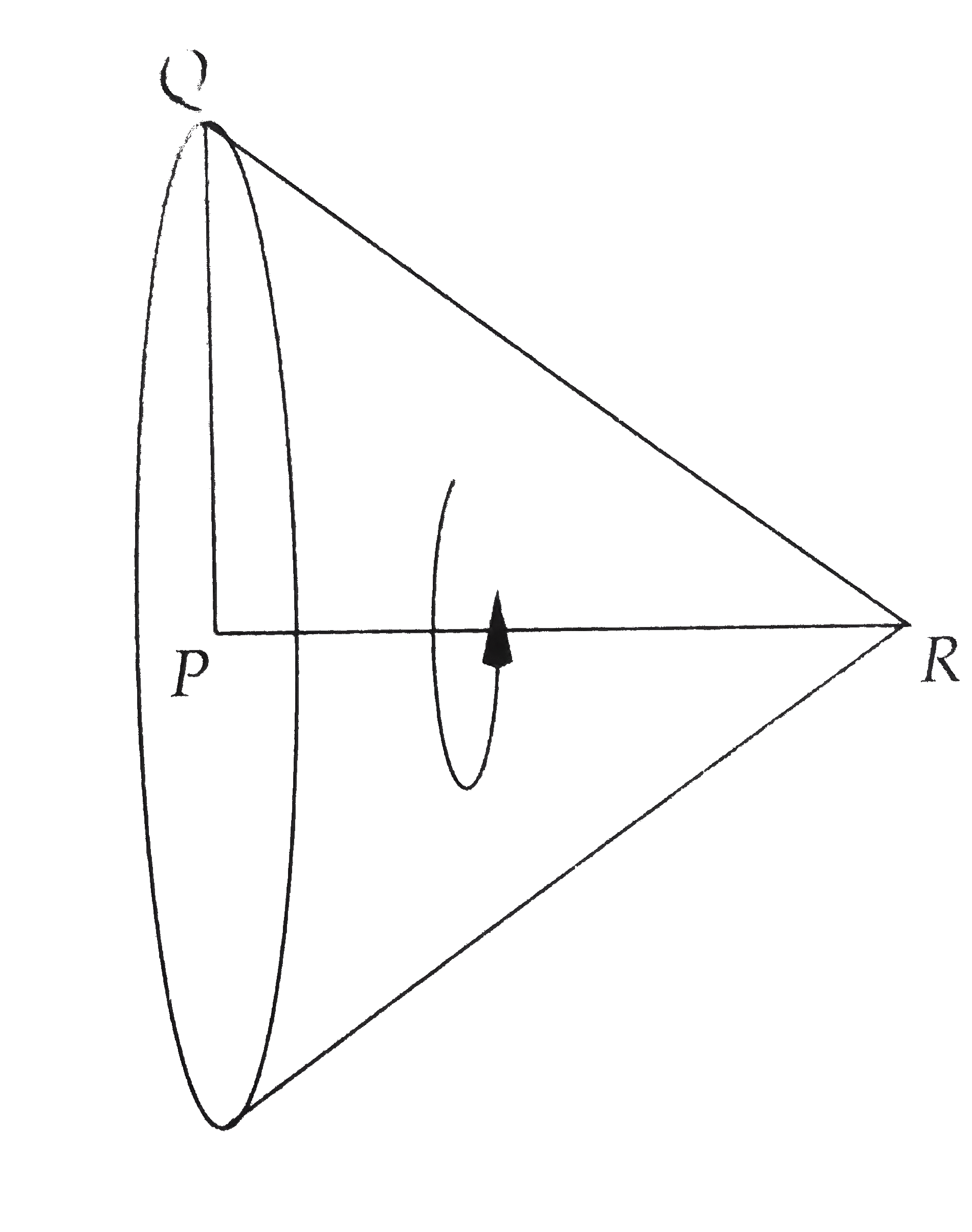
The resulting solid will be a right circular cone. The total surface area of a right circular cone is the sum of the area of the circular base plus the lateral area. If we call the radius of the circular base r, then the area of the circular base is `pi r^(2)`. If we cell the circumference of the circular base c and the slant height l, then the lateral area is `(1)/(2)cl`,
When right triangle PQR is rotated about PR, the resulting right circular cone will have a circular base with a radius that is leg PQ of right triangle PQR and a slant height that is hypotenuse QR of this triangle. So in order to find the total surface area of the right circular cone, we need to find the length of leg PQ and the length of hypotenuse QR of right triangle PQR.
Let's first the length of PQ. The area of any triangle is `(1)/(2)xx` base `xx` height. The area of a right triangle is `(1)/(2)xx "leg"_(1) xx "leg"_(2)` , because one leg can be considered to be the base and the other leg can be considered to be the height.
The area of right traingle PQR is `(1)/(2)xx(PR)xx(PQ)`. We know that PR = 4 and that area of right triangle PQR is 6. So `(1)/(2)xx4xx(PQ)=6`. Let's solve this equation for PQ. We have `2xx(PQ)=6`, so PQ = 3. The radius of the base of the right circular cone is 3. The area of the circular base is `pi(3^(2))=9 pi`.
Now let's find the hypotenuse QR of right triangle PQR. This triangle has legs of length 3 and 4, so this is a 3-4-5 right triangle. So the length of QR is 5. Thus, the slant height l of the right circular cone is 5. The circumference c of the circular base is `2pi r = 2pi (3) = 6pi`. Thus, `c = 6pi` and `l = 5`. The lateral area is `(1)/(2)cl=(1)/(2)(6pi)(5)=(3pi)(5)=15pi`. The area of the circular base is `9pi` and the lateral area is `15pi`. The total surface area is `9pi+15pi=24pi`. Now `24~~75.3982236862`. To the nearest hundredth, `24pi ~~ 75.40`. Choice (C ) is correct.
A typical SAT subject Test : Mathematics Level 2 will include one or two questions that entail visulazing.