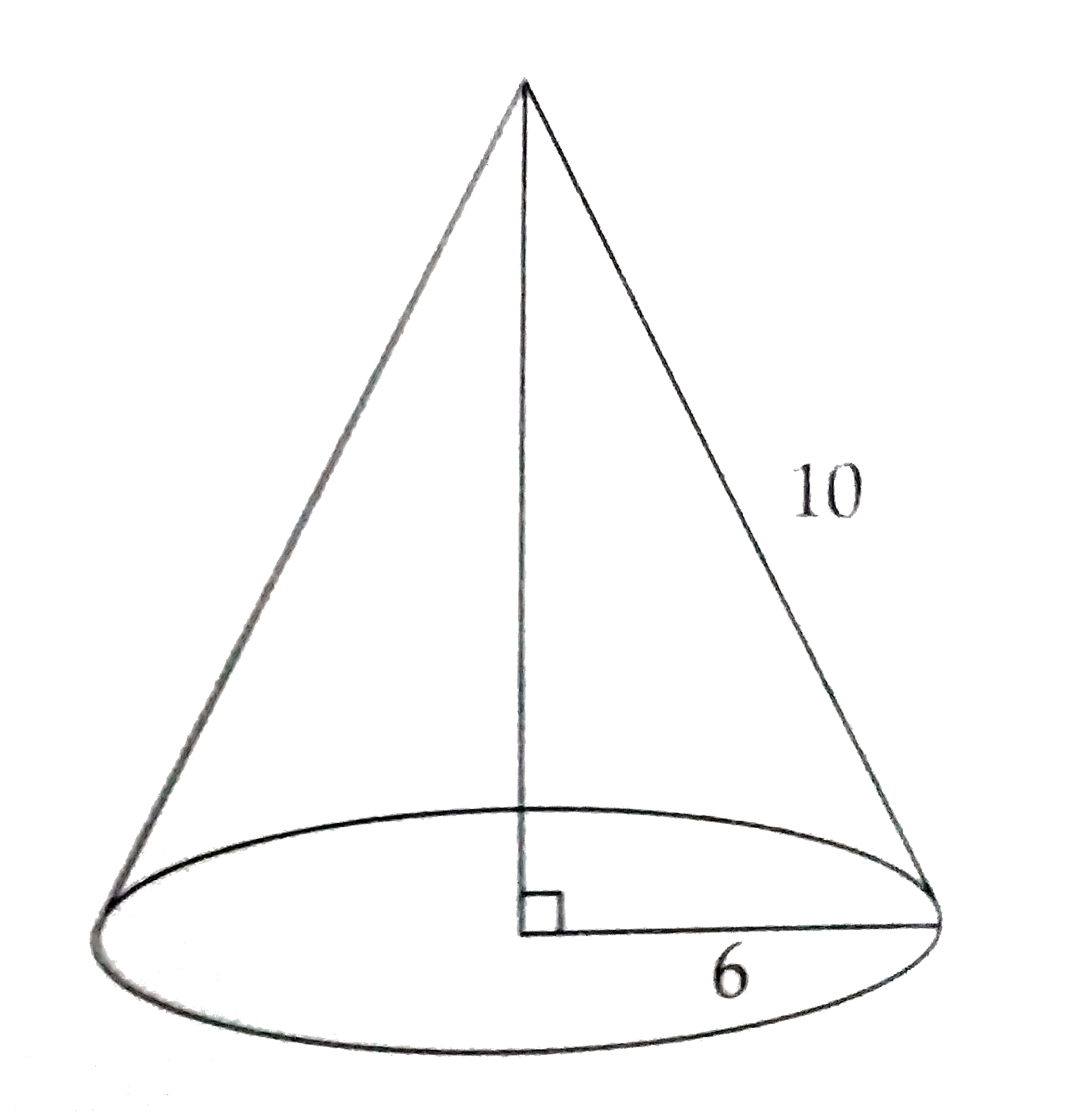
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
KAPLAN-SOLID GEOMETRY -SOLID GEOMETRY FOLLOW - UP TEST
- The lateral area of the right circular cone is 60pi. If the radius of ...
Text Solution
|
- D is the distance from vertex F to vertex G. The base is square, and t...
Text Solution
|
- A cube with edges of length b is divided into 8 equal smaller cubes. W...
Text Solution
|
- When a right triangle of area 4 is rotated 360^(@) about its longer l...
Text Solution
|
- The pyramid in Figure composed of a square base of area 16 and four is...
Text Solution
|