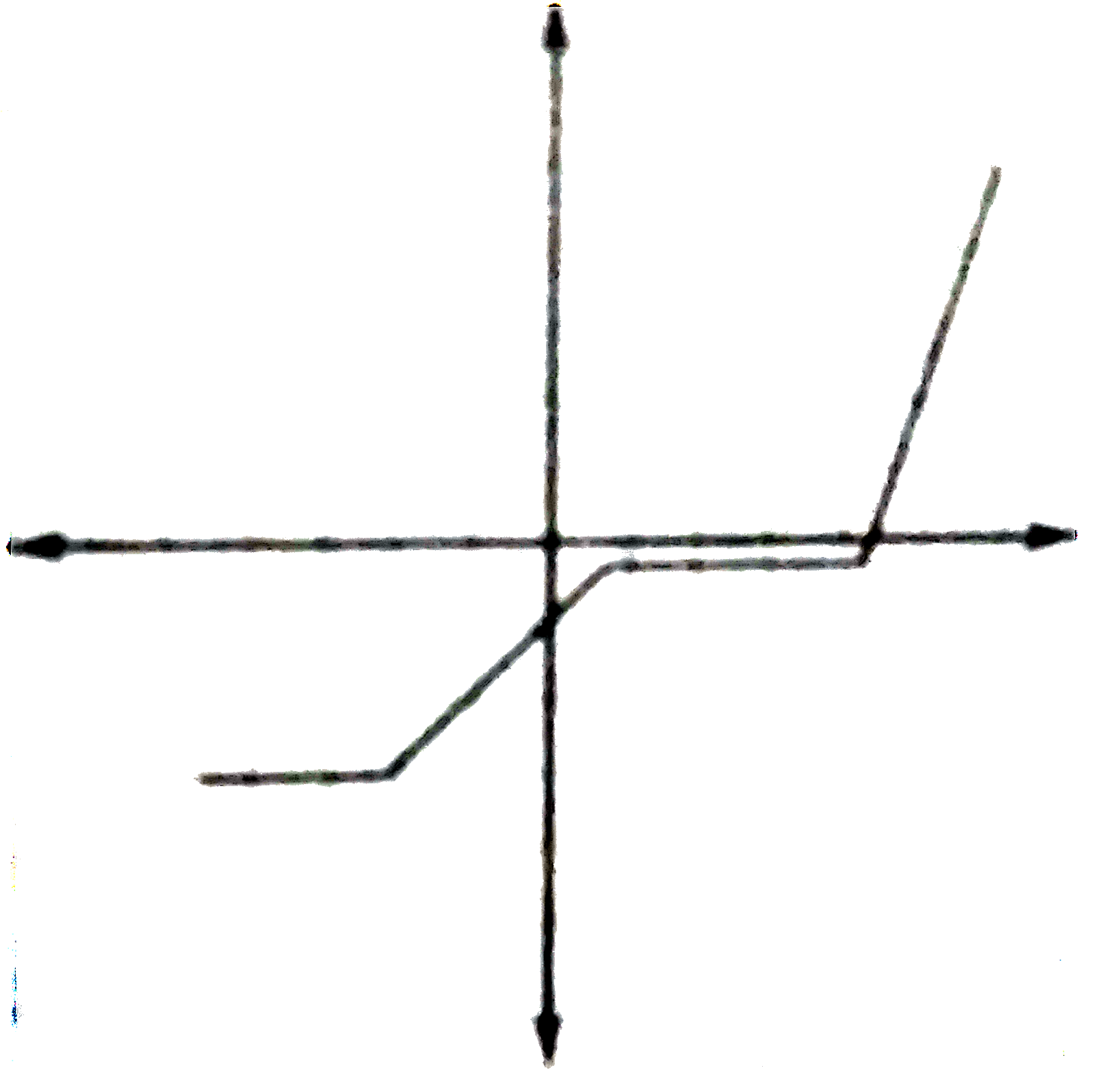
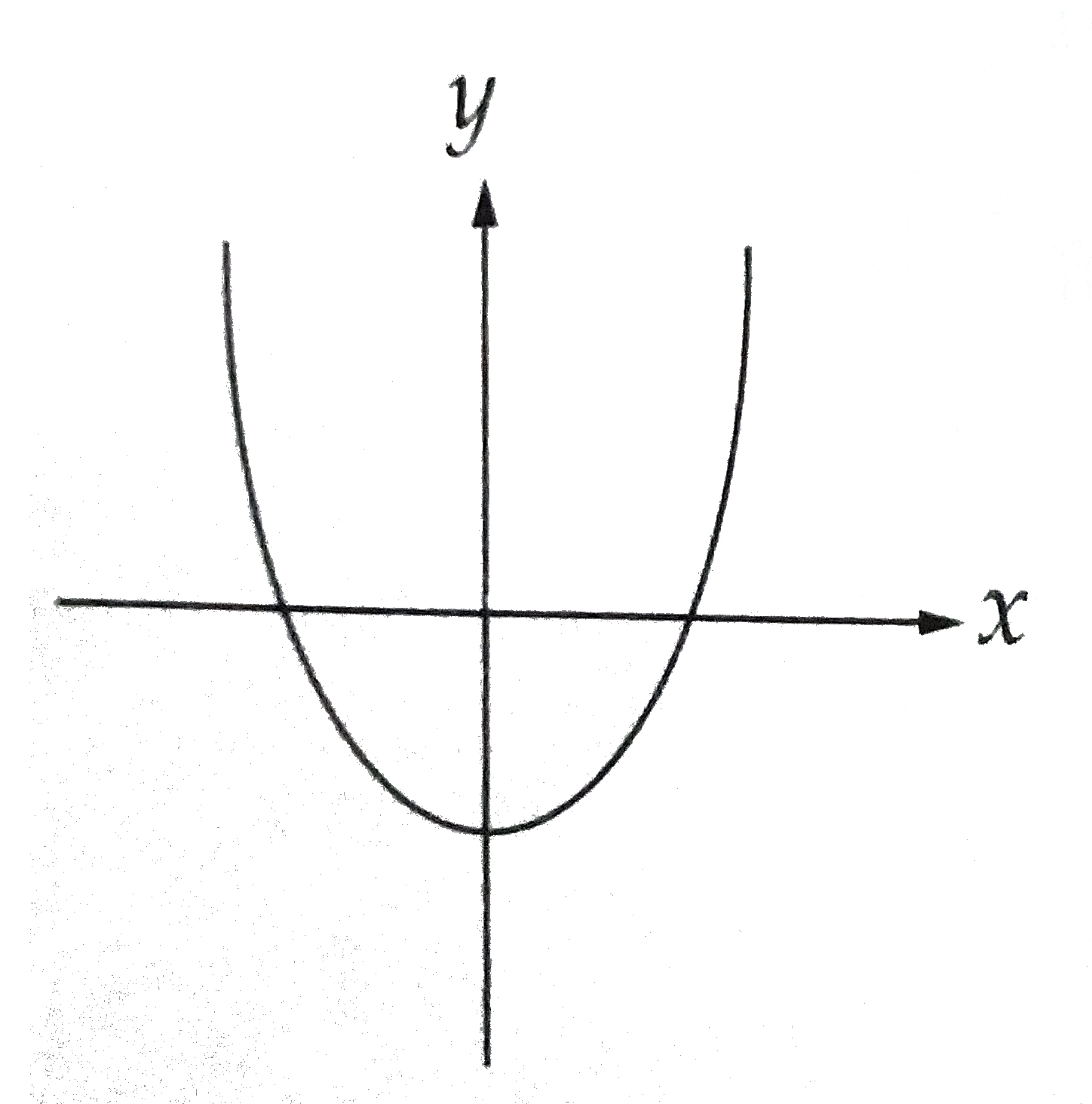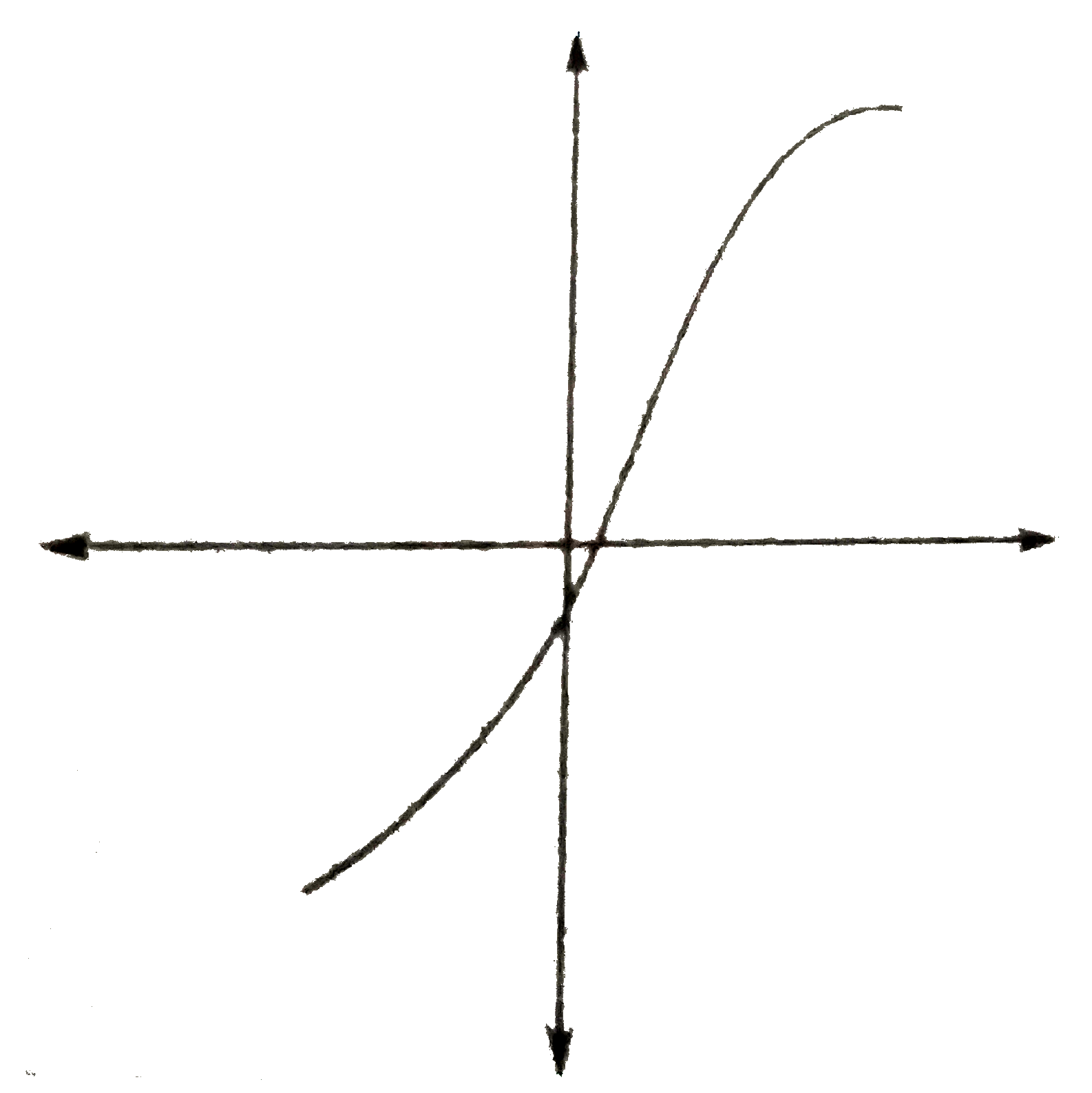A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
PLANE GEOMETRY
KAPLAN|Exercise PLANE GEOMETRY FOLLOW - UP TEST|6 VideosView PlaylistPRACTICE TEST 2
KAPLAN|Exercise PRACTICE TEST|50 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
KAPLAN-PRACTICE TEST 1 -PRACTICE TEST
- For all y ne 0, (1)/(y)+(1)/(2y)+(1)/(3y) =
01:01
|
Play - In a class of 10 boys and 15 girls, the average score on a biology tes...
01:55
|
Play - Which of the following graphs is symmetric about the origin ?
02:49
|
Playing Now - George is going on vacation and wishes to take along 2 books to read. ...
01:03
|
Play - If sqrt(3-x)-x=3,x=
01:42
|
Play - The lines with the equations y = m(1)x+4 and y = m(2)x+3 will intersec...
03:15
|
Play - If the probability that it will rain sometime on Monday is (1)/(3) and...
01:23
|
Play - If sin 2A = (1)/(2), then (1)/("2 sin A cos A")=
00:57
|
Play - What values for x would make (1)/(sqrt(x+1)) undefined ?
01:27
|
Play - If 02 le x le 2, the maximum value of f(x)=1-x^(2) is
01:43
|
Play - If f(x)=1-4x, and f^(-1)(x) is the inverse of f(x), then f(-3)f^(-1)(-...
01:27
|
Play - Which of the following polynomials, when divided by 3x+4, equals 2x^(2...
01:45
|
Play - Let |x| be defined to be the ''floor'' of x, where |x| is the greates...
02:59
|
Play - If log(2)x + log(2)x=7, then =
01:09
|
Play - If f(x)=(sqrt(x-1))/(x), what is the domain of f(x) ?
02:48
|
Play - How many ways can 2 identical red chairs and 4 identical blue chairs b...
01:18
|
Play - If a+b gt 0 and c+d gt 0, which of the following must be true ?
02:09
|
Play - If x gt 0, a = x cos theta, and b = x sin theta, then sqrt(a^(2)+b^(2)...
01:16
|
Play - If 0^(@)lt x lt 90^(@) and 5 sin^(2)x = 7 sin x - 2, what is the vlaue...
02:58
|
Play - 3-2i and 3+2i are roots to which of the following quadratic equations ...
02:27
|
Play