A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
TEST PAPERS
VIBRANT|Exercise PART-II : MATHEMATICS|20 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
VIBRANT-TEST PAPERS-PART - I : MATHEMATICS
- Suppose a,b in R. If the equation x^(2)-(2a+b)x+(2a^(2)+b^(2)-b+1//2)=...
02:56
|
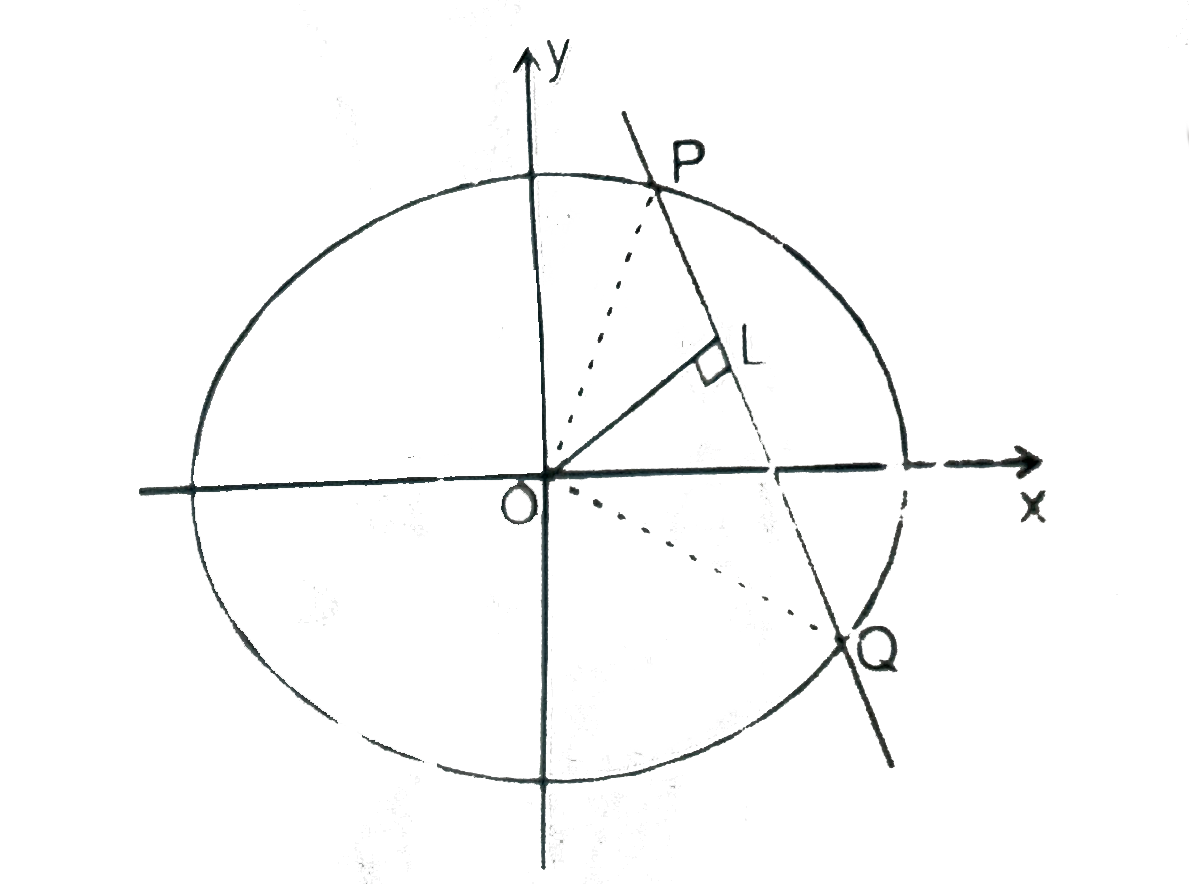
Playing Now - If alpha, beta are roots of x^(2)-2x-1=0, then value of 5alpha^(4)+12b...
07:44
|
Play - If 3p^(2)=5p+2 and 3q^(2)=5q+2 then the equation whose roots 3p-2p an...
06:57
|
Play - If 1 - p is a root of the quadratic equation x^(2) + px + 1- p = 0 , ...
03:01
|
Play - Sum of the series P=(1)/(2sqrt(1)+sqrt(2))+(1)/(3sqrt(2)+2sqrt(3))+......
04:46
|
Play - If a,b, c are in H.P. then a-(b)/(2),(b)/(2),c-(b)/(2) are in
03:01
|
Play - Sum of the series Sigma(r=1)^(n) rlog((r+1)/(r)) is
02:56
|
Play - Suppose for each n in N, 1^(4)+2^(4)+.........n^(4)=an^(5)+bn^(4)+cn^(...
02:54
|
Play - For any two complex numbers z1,z2 and any real numbers aa n db ,|a z1-...
01:48
|
Play - If (x+iy)^(1//3)=a+ib, " then " (x)/(a)+(y)/(b) equals
03:28
|
Play - The number of complex numbers z such that |z-1|=|z+1|=|z-i| is
04:16
|
Play - If |w|=2, then the set of points x+iy=w-(1)/(w) lie on
03:52
|
Play - If Delta(1)=|(x,b,b),(a,x,b),(a,a,x)|" and "Delta(2)=|(x,b),(a,x)|, th...
03:37
|
Play - Let Delta(x)=|(cos^(2)x,cosxsinx,-sinx),(cosxsinx,sin^(2)x,cosx),(sinx...
06:33
|
Play - Given, 2x - y + 2z = 2, x - 2y + z = -4, x + y+ lamda z = 4,then the v...
02:14
|
Play - Let A be a 3xx3 matrix such that A [(1,2,3),(0,2,3),(0,1,1)]=[(0,0,1),...
02:45
|
Play - Let A =[(1,1,0),(0,1,0),(0,0,1)] and let I denote the 3xx3 identity ma...
02:34
|
Play - If the standard deviation of the binomial distribution (q + p)^16 is 2...
03:54
|
Play - Suppose I+A is non-singular. Let B=(l+A)^(-1) and C=l-A, then ……. (wh...
03:25
|
Play - The number of ways of arranging 18 boys so that 3 particular boys are ...
03:02
|
Play