Home
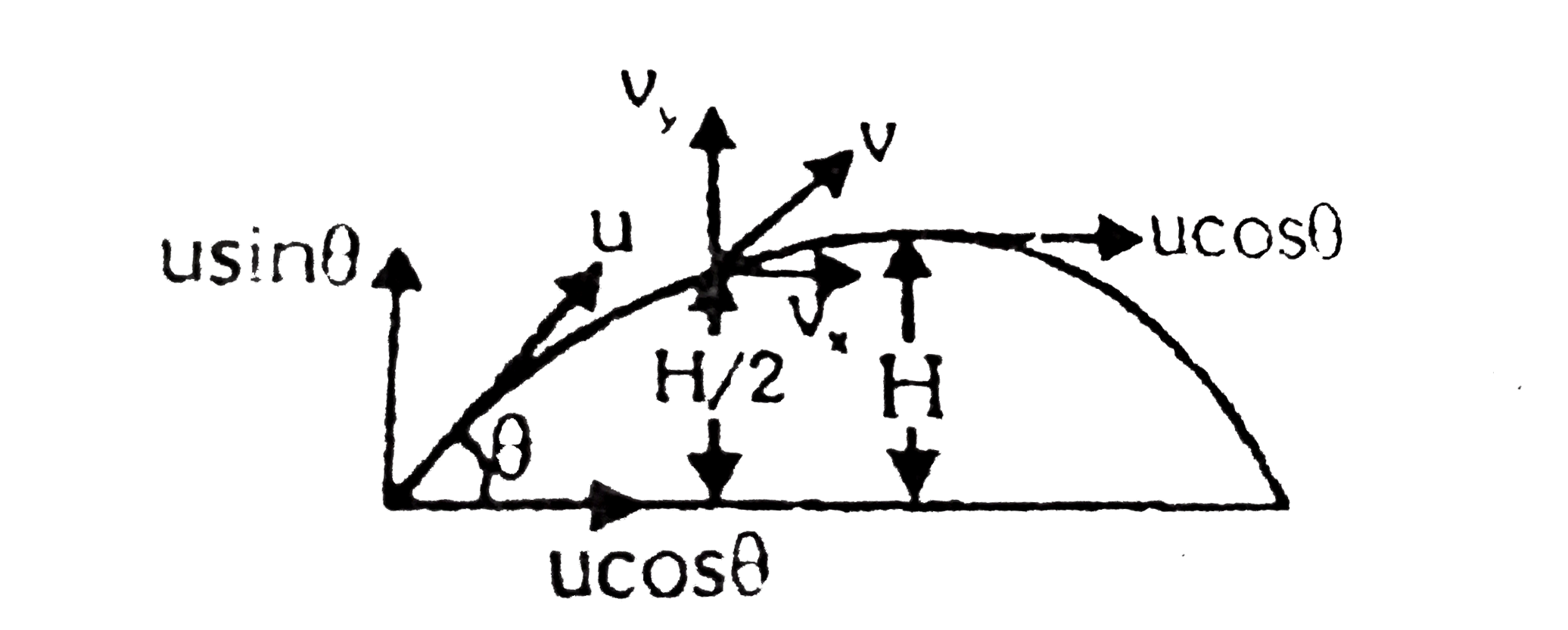
Class 11
PHYSICS
The total speed of a projectile at its g...

The total speed of a projectile at its greater height is `sqrt(6/7)` of its speed when it is at half of its greatest height. The angle of projection will be :-

A

`60^(@)`

B

`45^(@)`

C

`30^(@)`

D

`50^(@)`

Text Solution

Verified by Experts

The correct Answer is:
C
`v_(y)^(2)=u^(2)sin^(2)theta-2gxxH/2,v_(x)^(2)=u^(2) cos^(2) theta`

`:. U cos theta =sqrt(6/7)[sqrt(v_(x)^(2)+v_(y)^(2))]rArr cos theta=sqrt(3)/2` or `theta=30^(@)`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • KINEMATICS

    ALLEN|Exercise EXERCISE-02|57 Videos

  • KINEMATICS

    ALLEN|Exercise EXERCISE-03|6 Videos

  • KINEMATICS

    ALLEN|Exercise Integer Type Question|3 Videos

  • ERROR AND MEASUREMENT

    ALLEN|Exercise Part-2(Exercise-2)(B)|22 Videos

  • KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)

    ALLEN|Exercise BEGINNER S BOX-7|8 Videos

Similar Questions

Explore conceptually related problems

The velocity of a particle when at its greatest height is sqrt((2)/(5)) of its velocity when at half its greatest height. The angle of projection is 30^(@) .

The speed of a projectile at its maximum height is half of its initial speed. The angle of projection is .

Knowledge Check

  • The speed of a projectile when it is at its greatest height is sqrt(2//5) times its speed at half the maximum height. The angle of projection is

    A
    `30^(@)`
    B
    `60^(@)`
    C
    `45^(@)`
    D
    `tan^(-1)(3//4)`

  • The velocity of a projectile when it is at the greatest height is (sqrt (2//5)) times its velocity when it is at half of its greatest height. Determine its angle of projection.

    A
    `theta=30^@`
    B
    `theta=45^@`
    C
    `theta=60^@`
    D
    `theta=90^@`

  • The ratio of the speed of a projectile at the point of projection to the speed at the top of its trajectory is x. The angle of projection with the horizontal is

    A
    `sin^(1) x`
    B
    `cos^(-1)x`
    C
    `sin^(-1) (1//x)`
    D
    `cos^(-1) (1//x)`

    • Similar Questions

    Explore conceptually related problems

    The horizontal range of a projectile is times of its maximum height. Its angle of projection will be :-

    Choose the correct option (i) The speed of a projectile at its maximum height is half of its initial speed. The angle of projection is 60^(@) . (ii) A missile is fired for maximum range with an initial velocity of 20 m//s , the range of the missile is 40 m . (iii) A ball is projected with a kinetic energy E at an angle of 45^(@) to the horizontal. At the highest point during its flight, its kinetic energy will be E//2 . (iv) An object is projected at an angle of 45^(@) with horizontal. The horizontal range and the maximum height will be in the ratio 4:1

    The speed of a projectile at its maximum height is sqrt3//2 times its initial speed. If the range of the projectile is n times the maximum height attained by it, n is equal to :

    The horizontal range of a projectile is 4 sqrt(3) times its maximum height. Its angle of projection will be

    The horizontal range of a projectile is 4sqrt(3) times its maximum height. The angle of projection is

    Home
    Profile