A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
MASTER PRACTICE PROBLEM
BANSAL|Exercise Multiple objective|131 VideosView PlaylistMASTER PRACTICE PROBLEM
BANSAL|Exercise Subjective|107 VideosView PlaylistMASTER PRACTICE PROBLEM
BANSAL|Exercise Comphrehension|134 VideosView PlaylistFLUID MECHANICS
BANSAL|Exercise PYQS AIEEE|10 VideosView PlaylistSEMICONDUCTORS
BANSAL|Exercise CBSE Question|32 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
BANSAL-MASTER PRACTICE PROBLEM-Reasoning
- Statement-1: When a sphere is rolling without sliding it is possible t...
02:25
|
Play - Figure shows a rigid body that is mirror symmetric about a plane and r...
02:18
|
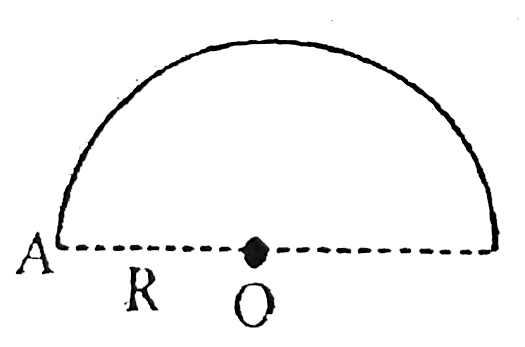
Play - Consider a semicircular ring with mass m and radius R as shown in figu...
Text Solution
|
Playing Now - Statement-1: For the calculation of gravitational force between any tw...
Text Solution
|
Play - Statement-1: Assuming zero potential at infinity, the gravitational po...
Text Solution
|
Play - Statement-1: Period of revolution of satellite in circular orbit aroun...
Text Solution
|
Play - Statement-1: It takes more fuel for a spacecraft to travel from the ea...
Text Solution
|
Play - A block of ice on earth floats on water with 9//10 of its volume subme...
03:18
|
Play - Statement-1: When an object is completely submerged in a liquid, the b...
05:51
|
Play - Statement-1: Coefficient of viscosity of liquid decreases while that o...
06:03
|
Play - In a standard resonance column experiment assuming negligible end corr...
03:35
|
Play - Two tunning forks produce a beat frequency of 2 Hz in air The same tun...
04:22
|
Play - Statement-1: Due to the motion of listener, the frequency of the sound...
04:16
|
Play - Statement-1: If the atmospheric pressure increases, sound travels fast...
02:53
|
Play - Statement-1: The level of water (initially at 0^(@)C) in a vessel (whi...
03:36
|
Play - Statement-1: At a steelworks, molten iron is heated to 1500^(@)C to re...
01:17
|
Play - Statement-1: Evaporation cools our body. Statement-2: When a body ra...
03:58
|
Play - Two identical objects A and B are at temperature T(A) and T(B) respect...
04:39
|
Play - Statement-1: A body is emitting primarily red light. As the temperatur...
03:58
|
Play - Statement-1: Two rigid, identical and uniformly charged non conducting...
Text Solution
|
Play