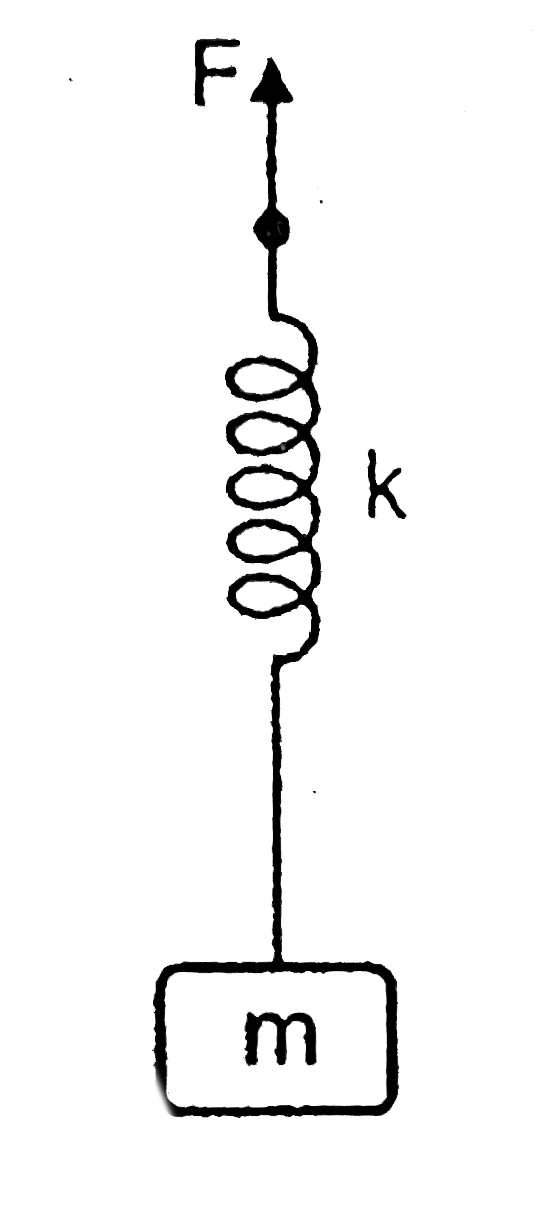
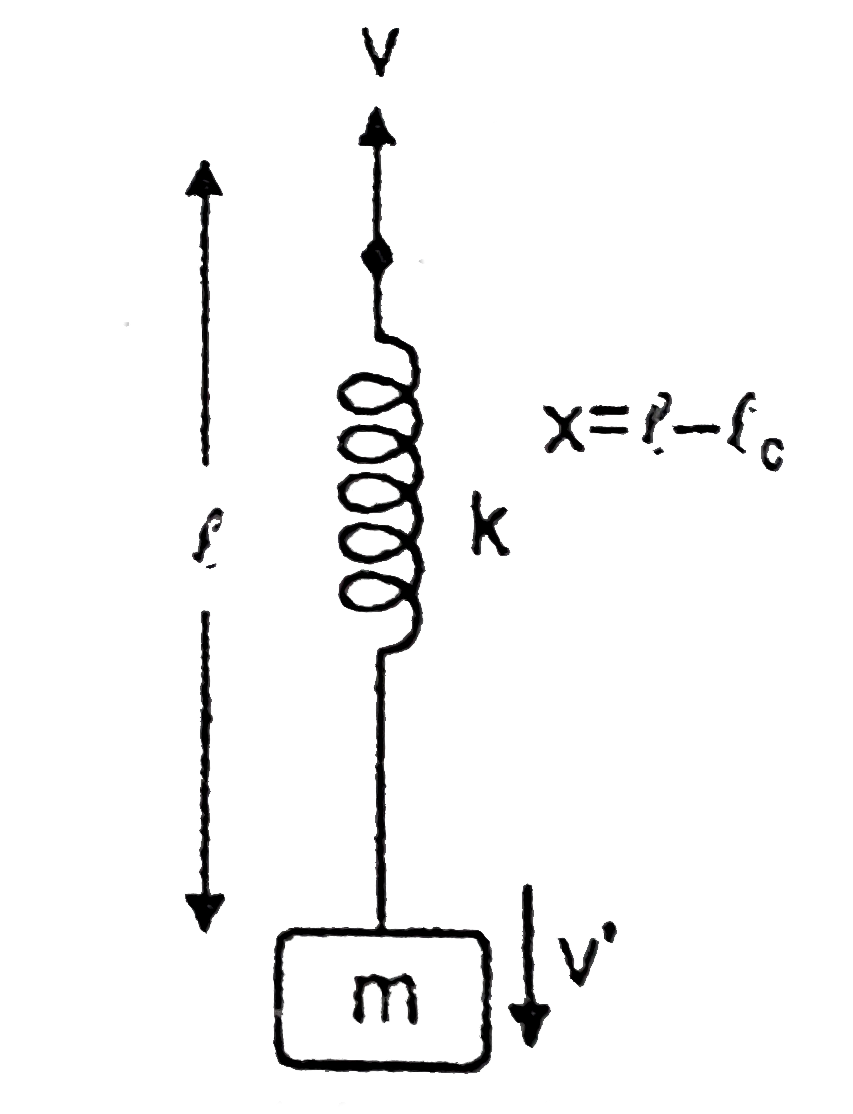
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
TEST PAPERS
RESONANCE|Exercise FST-3|30 VideosView PlaylistTRAVELLING WAVES
RESONANCE|Exercise Exercise- 3 PART II|7 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
RESONANCE-TEST SERIES-PHYSICS
- A time varying voltage is applied across A & B such that voltage acros...
02:22
|
Play - In a binary star system one of the stars has mass equal to mass of sun...
02:18
|
Play - A block of mass m is connected to a spring (spring constant k). Initia...
03:23
|
Playing Now - Two uniform solid spheres A and B of same material, painted completely...
03:48
|
Play - A particle moves along x-axis in positive direction. Its acceleration ...
04:28
|
Play - Consider a solid sphere of density rho and radius 4R. Centre of the sp...
02:11
|
Play - A semi circular disc of radius R is placed on a smooth horizontal surf...
03:12
|
Play - A wave pulse is generated at the bottom of a uniform string (of mass m...
03:15
|
Play - In the circuit shown key is closed at t=0 with capacitor initially unc...
02:59
|
Play - Consider a solid sphere placed in surrounding with small temperature d...
02:04
|
Play - Velocity time graphs of particles A and B moving along x-axis are show...
04:05
|
Play - Figure shows a conducting sphere with a cavity. A point charge q(1) is...
04:30
|
Play - In the figure shown capacitors A and B of capacitance C are in steady ...
10:05
|
Play - Which of these is/are representing electrostatic field? (x and y are ...
02:37
|
Play - The ends of copper rod of length 1m and area of cross section 1cm^(2) ...
05:40
|
Play - A sample of helium is undergoing a cyclic process ABCA as shown. In wh...
08:34
|
Play - In given circuit all capacitor were uncharged initially. First switch ...
04:17
|
Play - In given circuit all capacitor were uncharged initially. First switch ...
04:17
|
Play - A particle of mass 2kg moves under a force given by vec(F)=-(8N//m)(...
04:54
|
Play - A particle of mass 2kg moves under a force given by vec(F)=-(8N//m)(...
02:24
|
Play