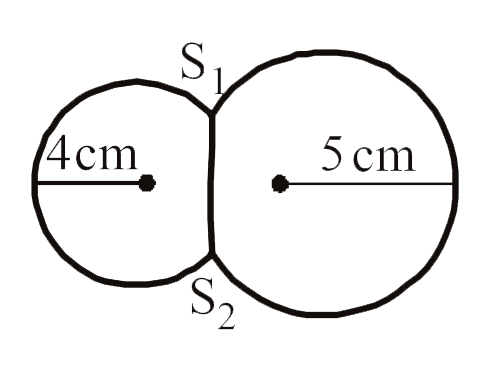Home
Class 12
PHYSICS
Two soap bubbles of radii r(1) and r(2) ...

Two soap bubbles of radii `r_(1)` and `r_(2)` equal to 4 cm and 5 cm are touching each other over a common surface `S_(1)S_(2)` (shown in figure). Its radius will be

A

4 cm

B

20 cm

C

5 cm

D

4.5 cm

Text Solution

Verified by Experts

The correct Answer is:
B
`r=(r_(1)r_(2))/(r_(2)-r_(1))`
Promotional Banner

Topper's Solved these Questions

  • DRILL TEST - 4

    NEET MAJOR TEST (COACHING)|Exercise PHYSICS|25 Videos

  • DRILL TEST 1

    NEET MAJOR TEST (COACHING)|Exercise PHYSICS|45 Videos

Similar Questions

Explore conceptually related problems

Two soap bubbles of radius r_(1) and r_(2) combine. Find radius of curvature of the common surface separating them.

When two soap bubbles of radius r_(1) and r_(2)(r_(2) gt r_(1)) coalesce, the radius of curvature of common surface is

Two soap bubbles of radii r_(1) and r_(2) are attached as shown. Find the radius of curvature of the common film ACB.

Two soap bubbles of radii 4cm and 6 cm are in contact with each other. What is the radius of the common boundary?

Two soap bubbles each of radius r are touching each other. The radius of curvature of the common surface will be:

Two soap bubbles of radii 2 cm and 3 cm are brought in contact. Find the radius of curvature (in cm) of the contact surface.

Two soap bubbles of radii 2 cm and 4 cm join to form a double bubble in air, then radius of. curvature of interface is

Two soap bubble of radii R_(1) and R_(2) are kept in vacuum at constant temperature, the ratio of masses of air inside them, is

Under isothermal condition two soap bubbles of radii r_(1) and r_(2) coalesce to form a single bubble of radius r. The external pressure is p_(0) . Find the surface tension of the soap in terms of the given parameters.

NEET MAJOR TEST (COACHING)-DRILL TEST -1-PHYSICS
  1. Two soap bubbles of radii r(1) and r(2) equal to 4 cm and 5 cm are to...

    Text Solution

    |

  2. Each of the four particles move along x axis. Their coordinates (in me...

    Text Solution

    |

  3. The random error in the arithmetic mean of 100 observations is x, then...

    Text Solution

    |

  4. A charge Q is distributed uniformly within the material of a hollow sp...

    Text Solution

    |

  5. The instant of time at which acceleration and velocity are perpendicul...

    Text Solution

    |

  6. A square loop with edge length 'a' meter. The resistance of wire ABC i...

    Text Solution

    |

  7. A physical quantity A is related to four observable a,b,c and d as fol...

    Text Solution

    |

  8. A circuit that contains three identical resistors with resistance R = ...

    Text Solution

    |

  9. An air column in a pipe, which is closed at one end will be in resonan...

    Text Solution

    |

  10. A potentiometer wire AB is 100 cm long and has total resistance of 10O...

    Text Solution

    |

  11. The volume of a block of a metal changes by 0.12% when it is heated th...

    Text Solution

    |

  12. The truth table for the following logic circuit is :-

    Text Solution

    |

  13. A Zener diode is connected to a battery and a load as shown below. The...

    Text Solution

    |

  14. An optical system consists of a thin convex lens of focal length 30 cm...

    Text Solution

    |

  15. The de-Brogile wavelength associated with electron in the n = 4 level ...

    Text Solution

    |

  16. The figure, shows a metre bridge circuit, with AB = 100 cm, x = 12 Ω ...

    Text Solution

    |

  17. Thre stones A, B and C are simultaneously projected from same point wi...

    Text Solution

    |

  18. In a sonometer wire the fundamental frequency of the wire is 260 Hz. I...

    Text Solution

    |

  19. If the energy levels of a hypothetical one electron atom are shown in ...

    Text Solution

    |

  20. In given circuit initially switch S(1) is closed for long time and th...

    Text Solution

    |