Home
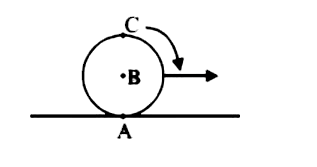
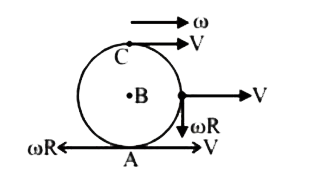
Class 12
PHYSICS
A sphere is rolling without slipping on ...

A sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then :

A

`vec(V)_(C^(-))vec(V)_(A=2)(vec(V)_(B^(-))vec(V)_(C ))`

B

`vec(V)_(C^(-))vec(V)_(B=)vec(V)_(B^(-))vec(V)_(A)`

C

`|vec(V)_(C^(-))vec(V)_(A)|=2|vec(V)_(B^(-))vec(V)_(C )|`

D

`|vec(V)_(C^(-))vec(V)_(A)|=4|vec(V)_(B)|`

Text Solution

Verified by Experts

The correct Answer is:
C
`vec(V)_(A)=V hat(i)+omega R(-hat(i)), vec(V)_(B)=V hat(i) , vec(V)_(C )=V hat(i)+ omega R hat(i)`
`vec(V)_(C )-vec(V)_(A)=2omega R hat(i)`
`2[vec(V)_(A)-vec(V)_(C )]=2[V(i)-V(i)-omega R(i)]=-2 omega R(i)`
Hence `vec(V)_(C )-vec(V)_(A)=-2(vec(V)_(B)-vec(V)_(C ))`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • ALLEN JEE SCORE AIOT TEST 2

    NEET MAJOR TEST (COACHING)|Exercise PHYSICS|25 Videos

  • DRILL TEST -1

    NEET MAJOR TEST (COACHING)|Exercise PHYSICS|24 Videos

Similar Questions

Explore conceptually related problems

Rolling (with and without slipping) on horizontal and inclined surface

A solid sphere is rolling without slipping on a horizontal plane. The ratio of its rotational kinetic energy and translational kinetic energy is

Knowledge Check

  • When a hollow sphere is rolling without slipping on a rough horizontal surface then the percentage of its total K.E. which is translational is

    A
    `72%`
    B
    `28%`
    C
    `60%`
    D
    `40%`

  • A 1 Kg solid sphere rolls without slipping on a rough horizontal suface as shown in figure. Select incorrect alternative

    A
    The acceleration of the centre of the sphere is `9.8 m//s^(2)`
    B
    The acceleration of the centre of the sphere is `10m//s^(2)`
    C
    The direction of frictional force on the sphere is towards right
    D
    The value of frictional force is 3N

  • Assertion: A disc rolls without slipping on a horizontal surface and the linear speed of its centre of mass is v. The rotational speed of the particles on its rim at the top of the disc will be 2v. Reason: The disc rolls as if it is rotating about the point of contact with the horizontal surface.

    A
    Assertion is True, Reason is True, Reason is a correct explanation for Assertion
    B
    Assertion is True, Reason is True, Reason is not a correct explanation for Assertion
    C
    Assertion is False but, Reason is True.
    D
    Assertion is True, Reason is False

    • Similar Questions

    Explore conceptually related problems

    A uniform sphere of radius R has a spherical cavity of radius (R)/(2) (see figure). Mass of the sphere with cavity is M. The sphere is rolling without sliding on a rough horizontal floor [the line joining the centre of sphere to the centre of the cavity remains in vertical plane]. When the centre of the cavity is at lowest position, the centre of the sphere has horizontal velocity V. Find: (a) The kinetic energy of the sphere at this moment. (b) The velocity of the centre of mass at this moment. (c) The maximum permissible value of V ( in the position shown ) which allows the sphere to roll without bouncing

    A disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v . Find the velocity of points A , B , C and D .

    A wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v . The velocity of a particle at the highest point of the rim is

    A solid sphere of mass m= 500gm is rolling without slipping on a horizontal surface. Find kinetic energy of a sphere if velocity of centre of mass is 5 cm/sec

    A solid sphere rolls without slipping along a horizontal surface. What percentage of its total kinetic energy is rotational kinetic energy?

    Home
    Profile