Consider a system of two particles of ma...

Consider a system of two particles of masses `m_(1)` and `m_(2)` separated by a distance r. Suppose they start to move towards each other due to their mutual attraction (attractive force may be electrical, gravitational, etc.).

Answer

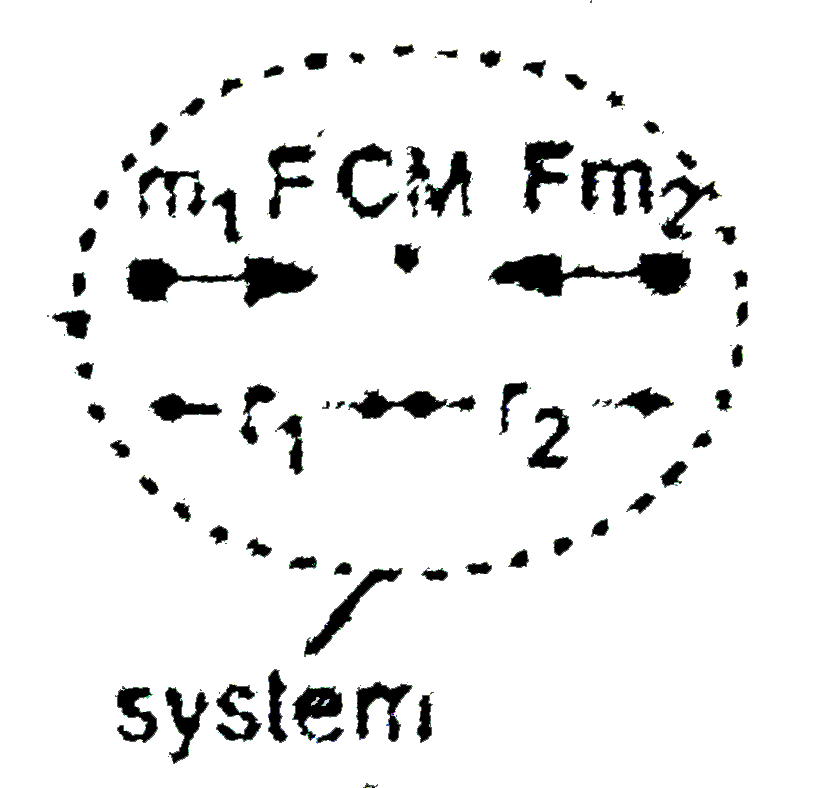
Step by step text solution for Consider a system of two particles of masses m_(1) and m_(2) separated by a distance r. Suppose they start to move towards each other due to their mutual attraction (attractive force may be electrical, gravitational, etc.). by PHYSICS experts to help you in doubts & scoring excellent marks in Class 11 exams.

Topper's Solved these Questions

IMPULSE AND MOMENTUM
ANURAG MISHRA|Exercise Example|50 Videos
IMPULSE AND MOMENTUM
ANURAG MISHRA|Exercise Level 1|110 Videos
FORCE ANALYSIS
ANURAG MISHRA|Exercise Matching type|13 Videos
RIGID BODY MOTION
ANURAG MISHRA|Exercise MATCH THE COLUMN|12 Videos

Two particles of masses 4kg and 6kg are separated by a distance of 20cm and are moving towards each other under mutual force of attraction, the position of the point where they meet is

`12 m`from `4kg` body

`12 m` from `6 kg` body

`8m` from `4 kg` body

`10 m` from `4 kg` body

In free space, two particles of mass m each are initially both at rest at a distance a from each other. They start moving towards each other due to their mutual gravitational attraction. The time after which the distance between them has reduced to (a)/(2) is:

`((pi+2)/(4sqrt(2)))((a^(3))/(Gm))^(1//2)`

`((pi-2)/(4sqrt(2)))((a^(3))/(Gm))^(1//2)`

`((pi+2)/(8))((a^(3))/(Gm))^(1//2)`

`((pi-2)/(8))((a^(3))/(Gm))^(1//2)`

Two bodies initially at rest, started moving towards each other due to mutual attraction. Which of the following is incorrect ?

`vec(a)_(cm) = 0`

`Sigma Delta vec(P) = 0`

`vec(v)_(cm) =` constant

None of these