Home
Class 11
PHYSICS
Assertion: Two blocks A and B are connec...

Assertion: Two blocks A and B are connected at the two ends of an ideal spring as shown in figure. Initially, spring was released. Now block B is pressed. Linear momentum of the system will not remain constant till the spring reaches its initial natural length.

Reason: An external force will act from the wall on block A.

A

If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.

B

If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.

C

If Assertion is true but Reason is false.

D

If Assertion is false but Reason is true.

Text Solution

Verified by Experts

The correct Answer is:
A
Linear momentum will not remain constant till spring will remain compressed. Therefore a force will act on block A from the wall.
Promotional Banner

Topper's Solved these Questions

  • CENTRE OF MASS

    DC PANDEY|Exercise Match the coloumns|9 Videos

  • CENTRE OF MASS

    DC PANDEY|Exercise Medical entrances gallery|27 Videos

  • CENTRE OF MASS

    DC PANDEY|Exercise Taking it together|73 Videos

  • CALORIMETRY AND HEAT TRANSFER

    DC PANDEY|Exercise Medical entrance s gallery|38 Videos

  • CENTRE OF MASS, IMPULSE AND MOMENTUM

    DC PANDEY|Exercise Comprehension type questions|15 Videos

Similar Questions

Explore conceptually related problems

Find the maximum tension in the spring if initially spring at its natural length when block is released from rest.

Two blocks having masses 8kg and 16kg are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible string also connects B with ceiling as shown in the figure at the initial moment. Initially the spring has its natural length. A constant horizontal force F is applied to the heavier block as shown. What is the maximum possible value of F so the lighter block doesn't loose contact with ground?

Two blocks having masses 8 kg and 16 kg are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible starting also connects B with ceiling as shown in figure at the initial moment. Initially the spring has its natural length. A constant horizontal force F is applied to the heavier block as shown. What is the maximum possible value of F so the lighter block doesn't loose contant with ground

Two blocks are connected to the two free ends of a spring of spring constant K . Both the blocks are moved apart to extend the psring beyond its natural length and then released . In subsequent motion

The system of the wedge and the block connected by a massless spring as shown in the figure is released with the spring in its natural length. Friction is absent. Maximum elongation in the spring will be

Two blocks A and B of mass m and 2m are connected together by a light spring of stiffness k . The system is lying on a smooth horizontal surface with block A in contact with a fixed vertical wall as shown in the figure. The block B is pressed towards the wall by a distance x_0 and then released. There is not friction anywhere. If spring takes time Deltat to aquire its natural length then average force on the block A by the wall is

DC PANDEY-CENTRE OF MASS-Assertion and reason
  1. These questions consists of two statements each printed as Assertion a...

    Text Solution

    |

  2. Assertion: A given force applied in turn to a number of different mass...

    Text Solution

    |

  3. Assertion: In inelastic collision, linear momentum of system does not ...

    Text Solution

    |

  4. Assertion: Two spherical bodies of mass ratio 1:2 travel towards each ...

    Text Solution

    |

  5. Assertion: Center of mass and center of gravity of a body will coincid...

    Text Solution

    |

  6. Assertion: A projectile gets exploded at its highest point. All the pi...

    Text Solution

    |

  7. Assertion: If a projectile explodes in mid air, linear momentum of cen...

    Text Solution

    |

  8. Assertion: When a body dropped from a height explodes in mid air, its ...

    Text Solution

    |

  9. Assertion: The centre mass of an electron and proton, when released mo...

    Text Solution

    |

  10. Assertion: The relative velocity of the two particles in head-on elast...

    Text Solution

    |

  11. Assertion: If net force on a system is zero, then momentum of every in...

    Text Solution

    |

  12. Assertion: If a projectile explodes in mid air, then no external force...

    Text Solution

    |

  13. Assertion: Two bodies moving in opposite directions with same magnitud...

    Text Solution

    |

  14. Assertion: A body is thrown with a velocity u inclined to the horizont...

    Text Solution

    |

  15. Assertion : A moving ball having an inelastic collison withh another m...

    Text Solution

    |

  16. Assertion: A rocket launched vertically upward explodes at the highest...

    Text Solution

    |

  17. Assertion: Two blocks A and B are connected at the two ends of an idea...

    Text Solution

    |

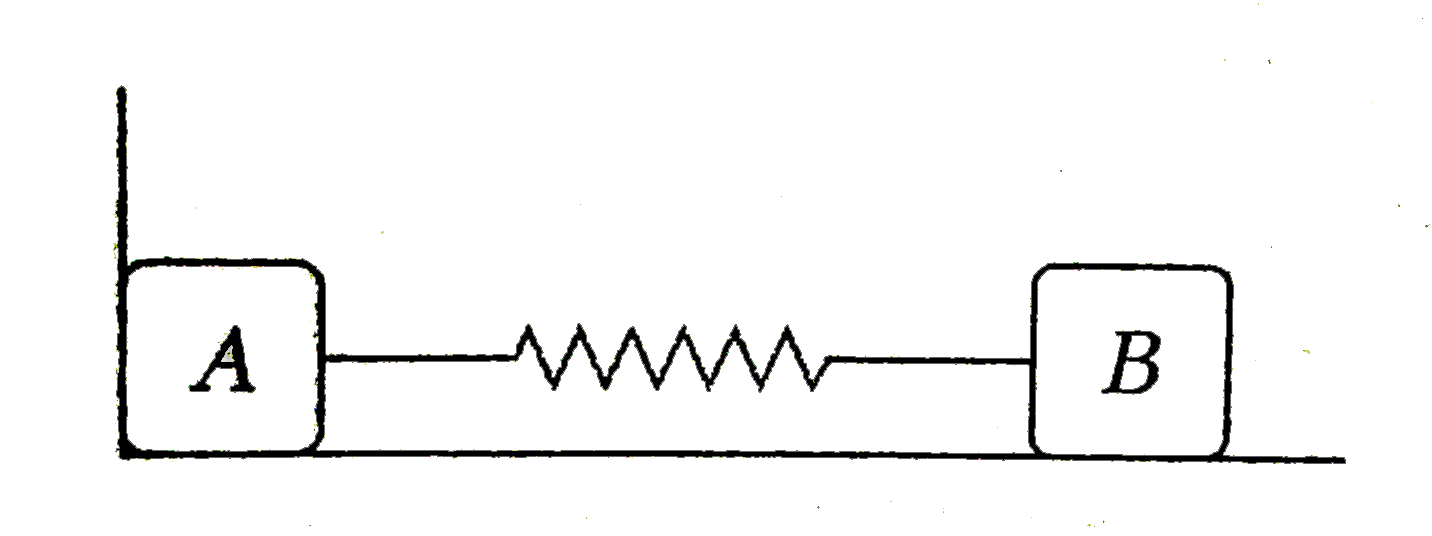
  18. Assertion: In the figure shown, linear momentum of system (of blocks A...

    Text Solution

    |

  19. Assertion: Two blocks of masses m(A) and m(B) (gtm(A) are thrown towar...

    Text Solution

    |

  20. Assertion: Two identical spherical spheres are half filled with two l...

    Text Solution

    |