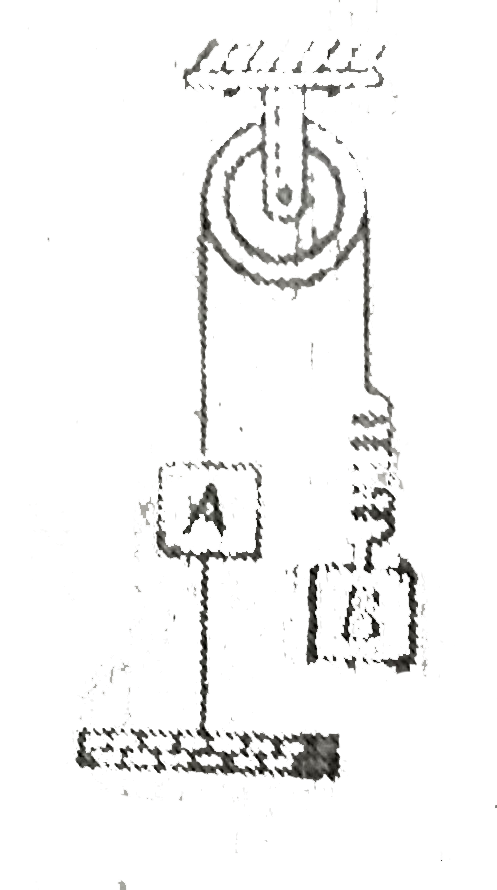Home
Class 11
PHYSICS
Blocks A and B shown in the figure are h...

Blocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is

A

g

B

`(g)/(2)`

C

2g

D

zero

Text Solution

Verified by Experts

Promotional Banner

Topper's Solved these Questions

  • CENTRE OF MASS, IMPULSE AND MOMENTUM

    DC PANDEY|Exercise More a than one option is Correct|1 Videos

  • CENTRE OF MASS, IMPULSE AND MOMENTUM

    DC PANDEY|Exercise Comprehension type questions|15 Videos

  • CENTRE OF MASS, IMPULSE AND MOMENTUM

    DC PANDEY|Exercise Comprehension type questions|15 Videos

  • CENTRE OF MASS

    DC PANDEY|Exercise Medical entrances gallery|27 Videos

  • CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION

    DC PANDEY|Exercise Level 2 Subjective|21 Videos

Similar Questions

Explore conceptually related problems

In the shown diagram mass of A is m and that of B is 2 m. All the surfaces are smooth. System is released from rest with spring unstretched. Then, the maximum extension (x_(m)) in spring will be:

Initially block shown is at rest and the spring is unstretched, when a constant force F begins to act on it neglect friction. Find maximum extension in the spring

The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N//m . In the equilibrium position, speed of the block placed horizontally is

The system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k = 100 N//m , then maximum extension in spring is :

Consider the situation shown in figure. Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find (a) The maximum extension of the spring x_(m) (b) The speed of block A when the extension in the springt is x=(x_(m))/(2) (c ) The net acceleration of block B when extension in the spring is x=(x_(m))/(4).

The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

In the figure shown, the system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m. Maximum speed of the block placed horizontally is:

An ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is

The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N//m . Extension of horizontal spring in equilibrium is

DC PANDEY-CENTRE OF MASS, IMPULSE AND MOMENTUM-Only one option is correct for JEE Advanced
  1. A small ball falling vertically downward with constant velocity 2m//s ...

    Text Solution

    |

  2. Two blocks of mass m and 2m are kept on a smooth horizontal surface. T...

    Text Solution

    |

  3. Blocks A and B shown in the figure are having equal masses m. The syst...

    Text Solution

    |

  4. Both the blocks as shown in figure are given together a horizontal vel...

    Text Solution

    |

  5. A particle of mass 3m is projected from the ground at some angle with ...

    Text Solution

    |

  6. A girl throws a ball with an initial velocity v at an angle 45^@. The ...

    Text Solution

    |

  7. A ball collides at B with velocity 10m//s at 30^(@) with vertical. The...

    Text Solution

    |

  8. The lower end of a 4 m long uniform rod AB is pulled with constant spe...

    Text Solution

    |

  9. A rigid rod leans against a vertical wall (y-axis) as shwon in figure....

    Text Solution

    |

  10. A bullet of mass m moving vertically upwards instantaneously with a ve...

    Text Solution

    |

  11. A super-ball of mass m is to bounce elastically back and forth between...

    Text Solution

    |

  12. A block of mass M with a semicircualr of radius R, rests on a horizont...

    Text Solution

    |

  13. A block of mass M with a semicircualr of radius R, rests on a horizont...

    Text Solution

    |

  14. A skater of mass m standing on ice throws a stone of mass M with a vel...

    Text Solution

    |

  15. A small ball on a frictionless horizontal surface moves towards right ...

    Text Solution

    |

  16. A body of mass m is dropped from a height of h. Simultaneously another...

    Text Solution

    |

  17. Two bars of masses m1 and m2 connected by a weightless spring of stiff...

    Text Solution

    |

  18. A rocket is projected vertically upwords. It explodes at the/ topmost ...

    Text Solution

    |

  19. A raindrop as it falls through for or mist collects mass at a uniform ...

    Text Solution

    |

  20. A small block of mass 'm' is placed on bigger block of mass M(1) which...

    Text Solution

    |