Home
Class 12
CHEMISTRY
Find out X:...


Find out X:

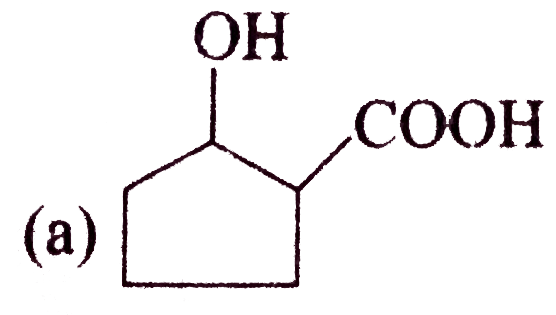
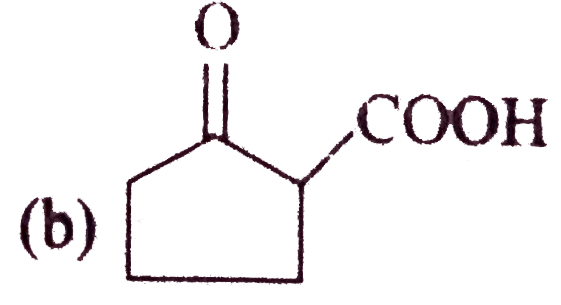
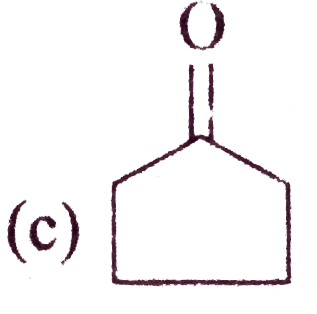
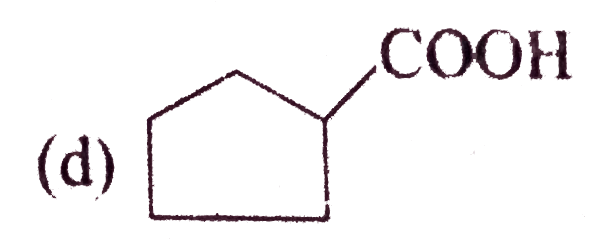
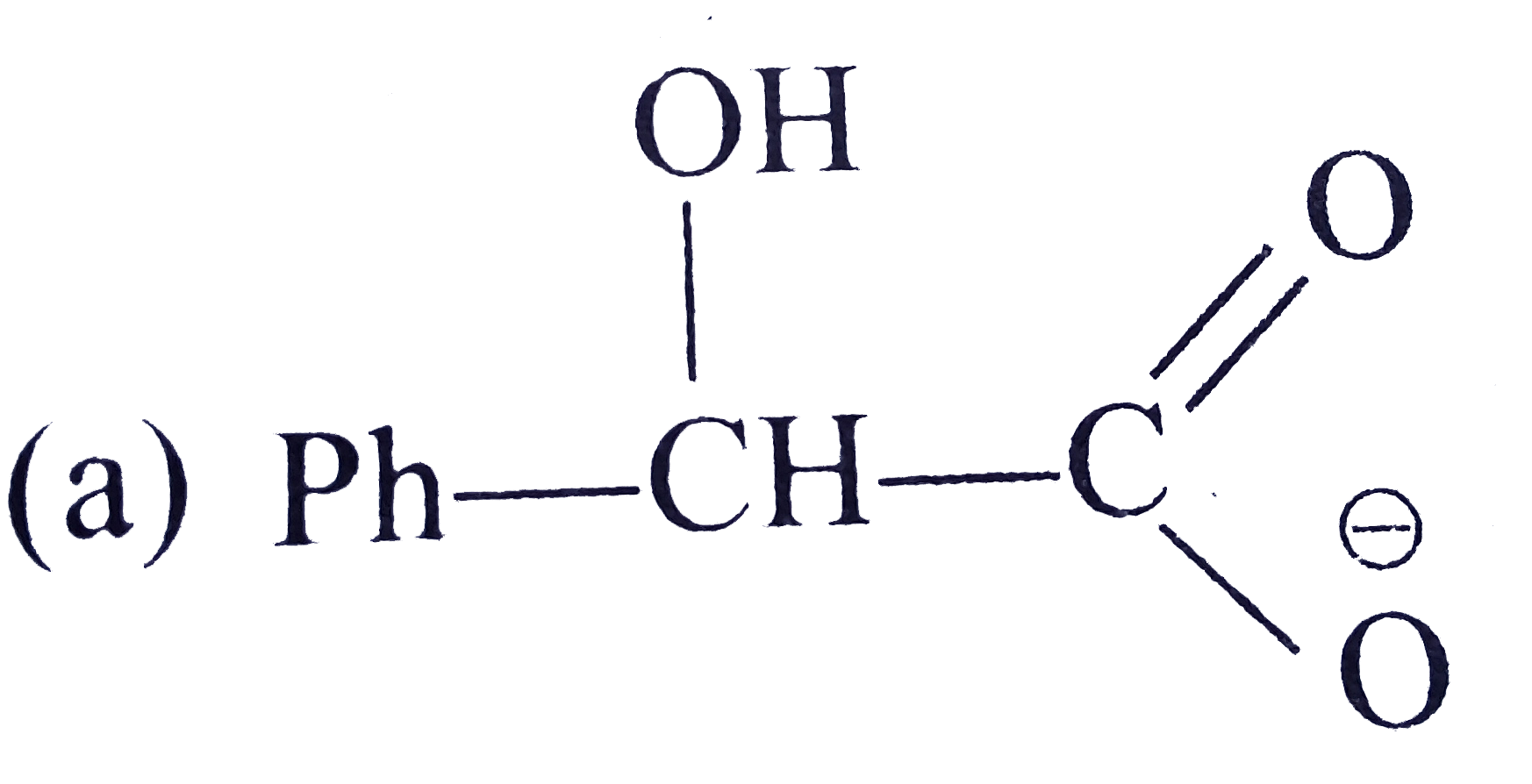
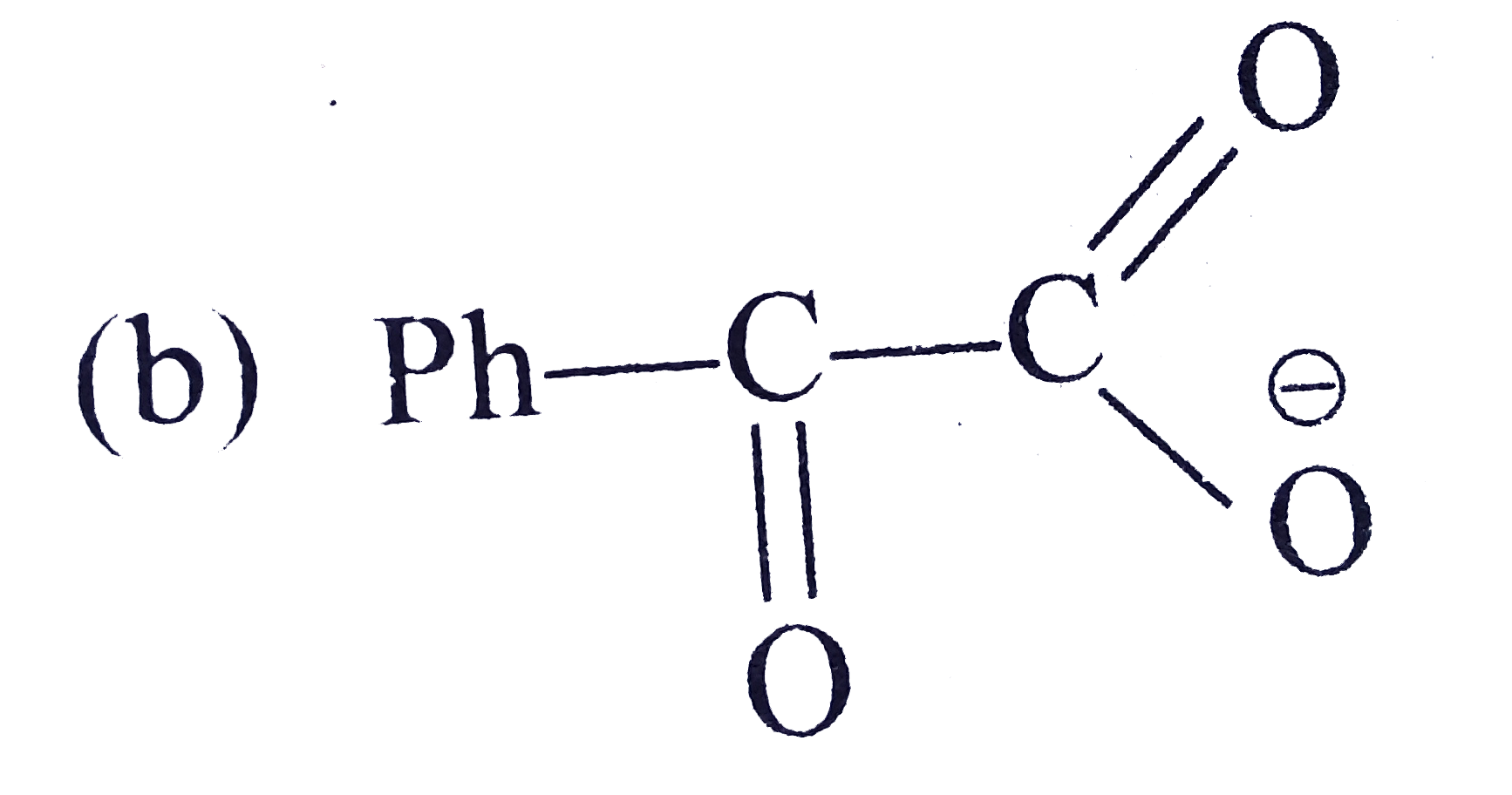
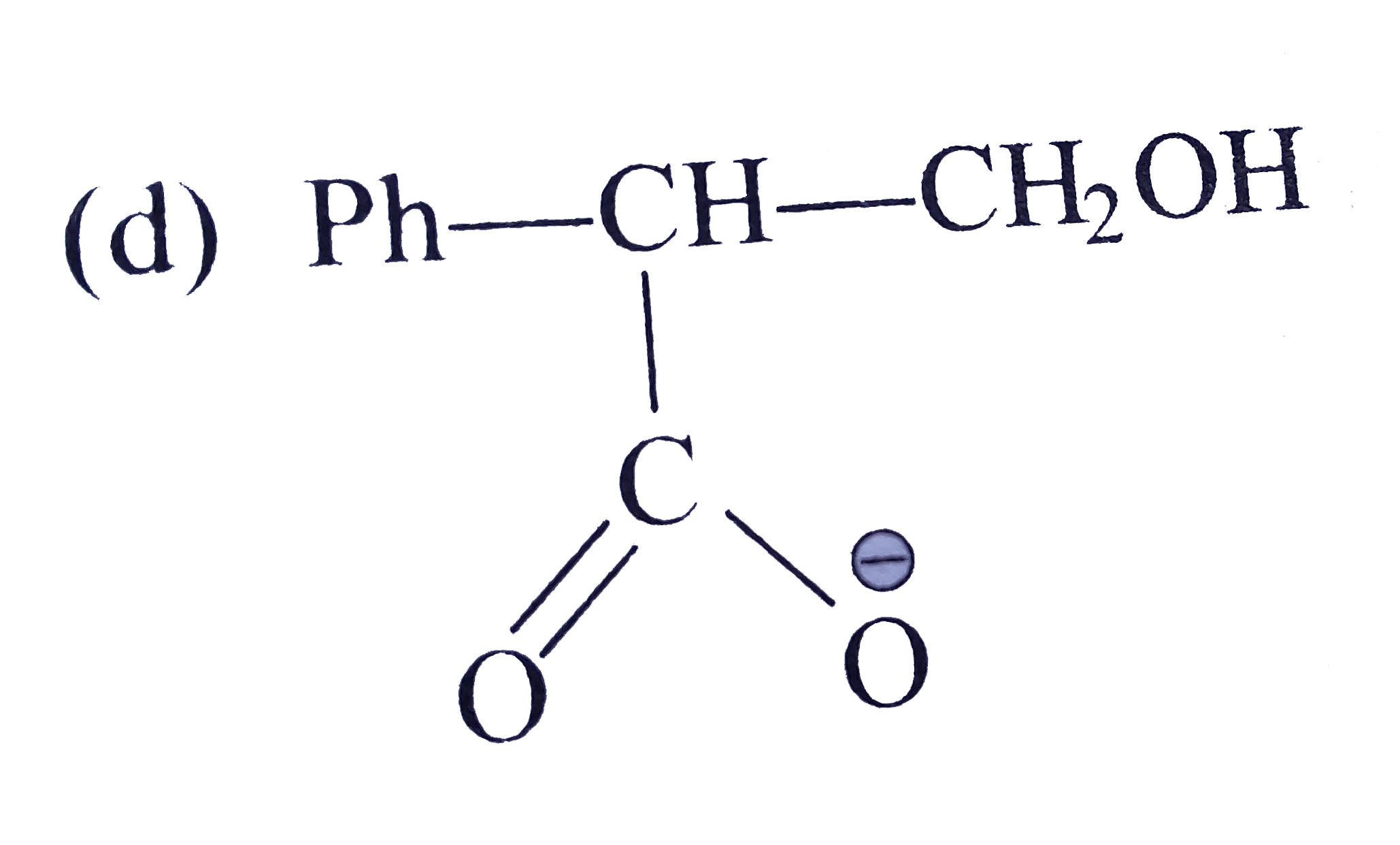
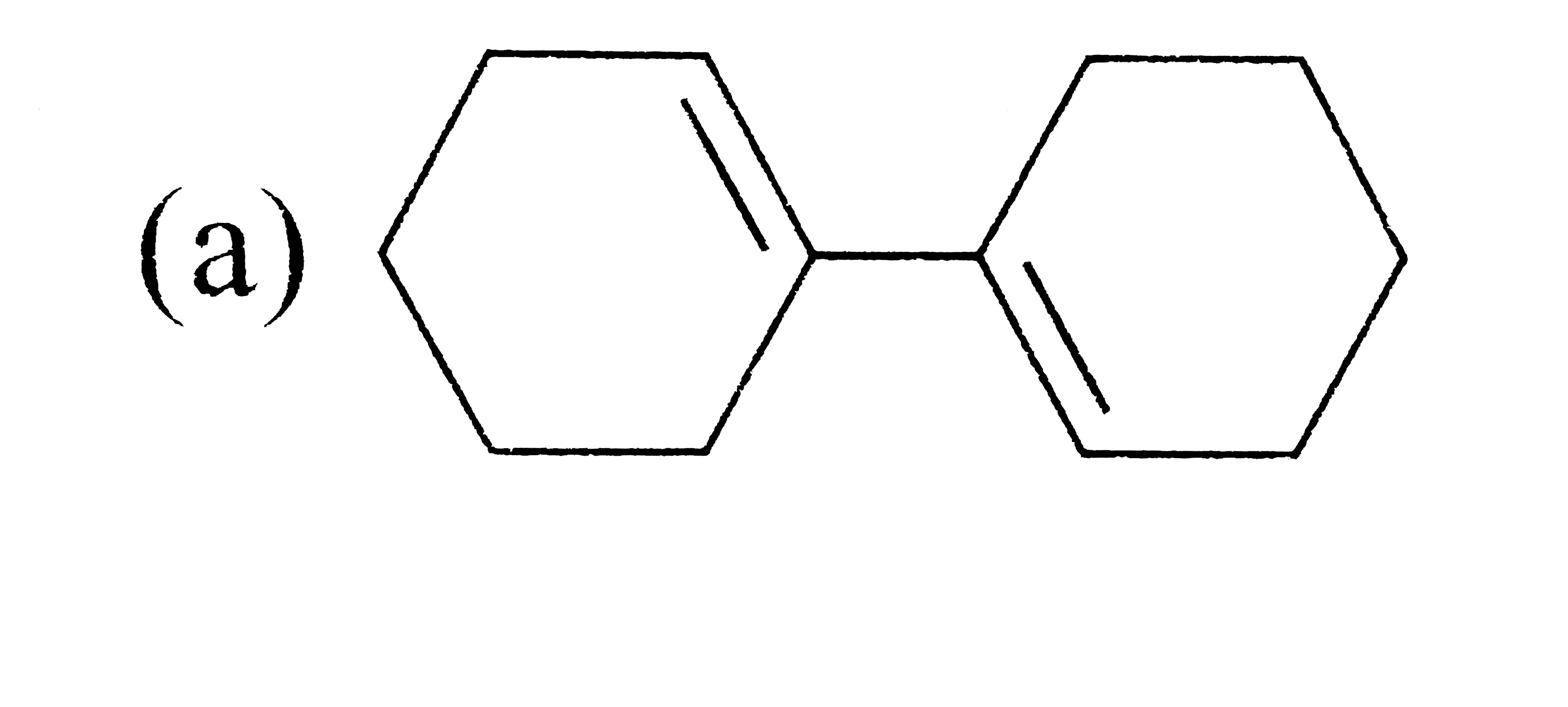
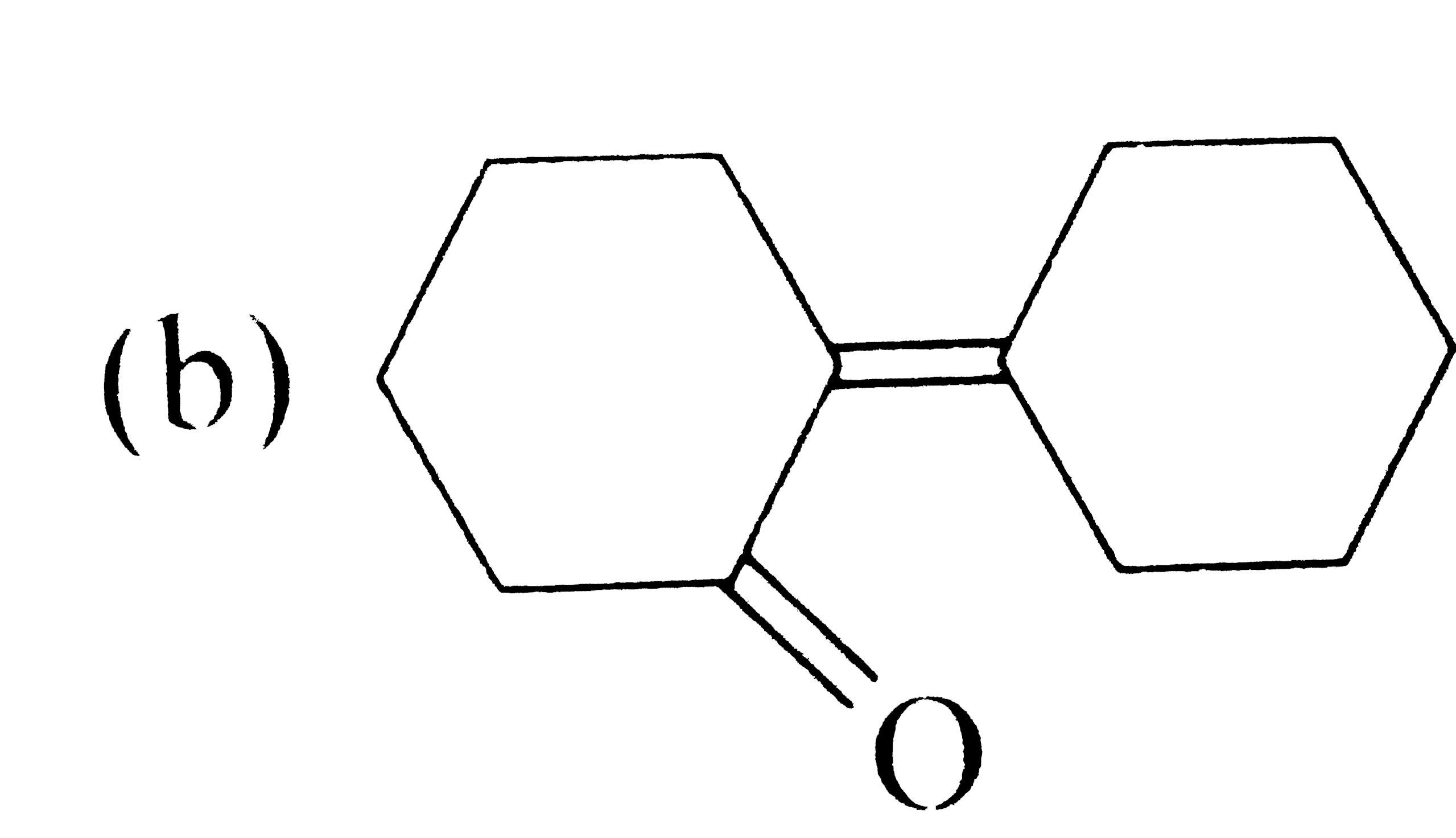
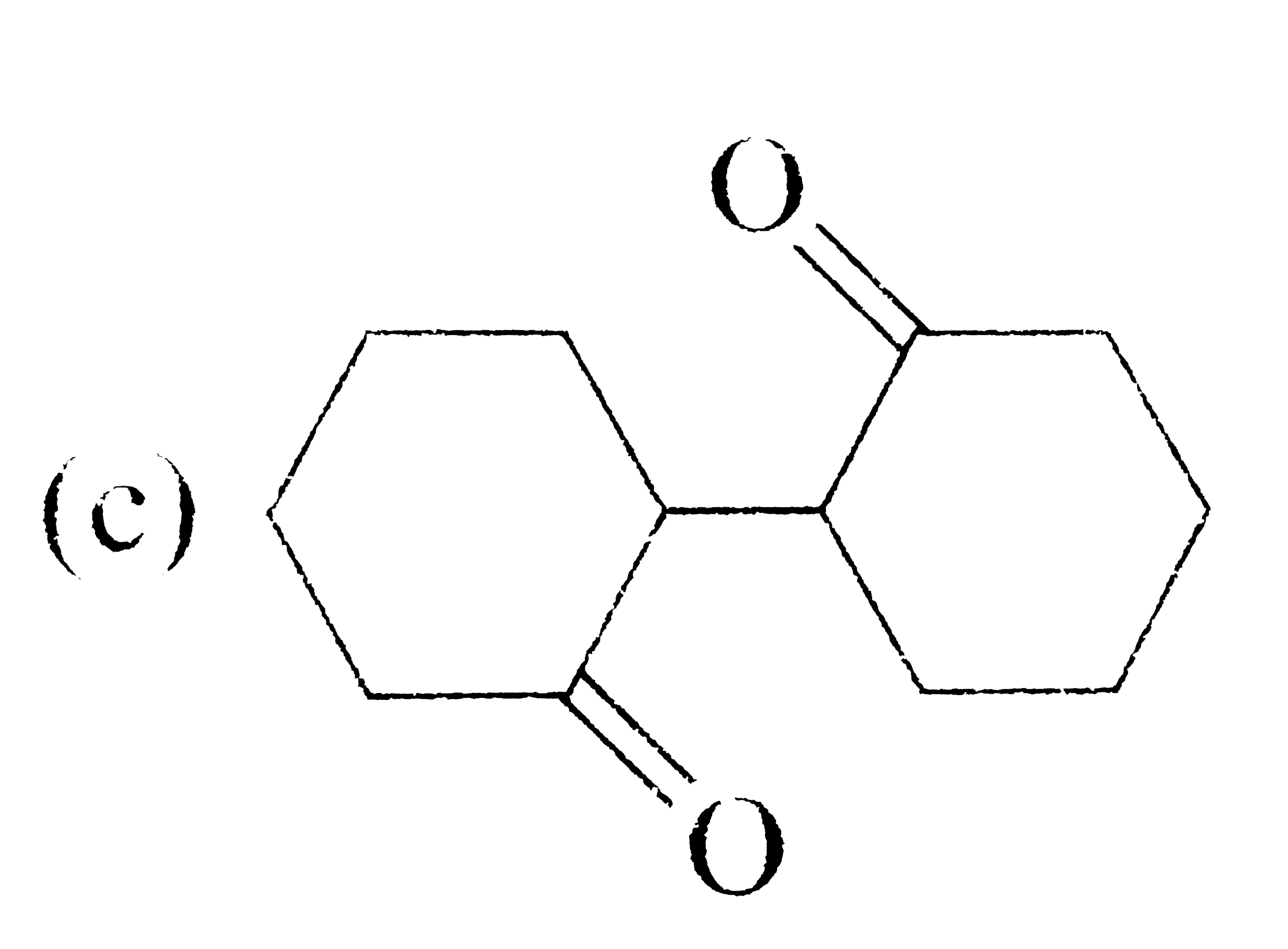
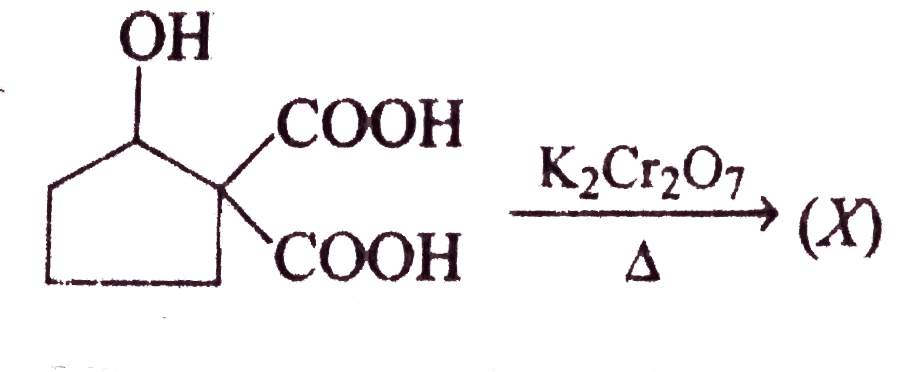A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
C
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • ALCOHOLS AND ETHERS

    GRB PUBLICATION|Exercise level 28|1 Videos

  • ALCOHOLS AND ETHERS

    GRB PUBLICATION|Exercise level 29|1 Videos

  • ALCOHOLS AND ETHERS

    GRB PUBLICATION|Exercise level 26|1 Videos

  • ALCOHOL, ETHER AND EPOXY

    GRB PUBLICATION|Exercise STRAIGHT OBJECTIVE TYPE|22 Videos

  • BIOMOLECULES, POLYMERS, PRACTICAL ORGANIC CHEMISTRY AND CHEMISTRY IN DAILY LIFE

    GRB PUBLICATION|Exercise SUBJECTIVE TYPE|40 Videos

Similar Questions

Explore conceptually related problems

, Find out the value of 'X'

The demand function of a commodity x is given by Q_(X) = 20 - 3P_(X) . Find out the values of P_(X) , when corresponding values of Q_(X) are given as : 5, 8, 11 and 14.

Knowledge Check

  • When an aldehyde with no alpha -hydrogen react with concentrated aqueous NaOH, half the aldehyde is converted ot carboxylic acid salt and other half is converted to an alcoho. In other words, half the reaction is oxidized and other half is reduced. This reaction is known as Cannizzaro reaction Find out 'X'of the reaction :

    A
    B
    C
    `Ph-overset(O)overset(||)C-CH_(2)OH`
    D

  • , Find out final product (X) :

    A
    B
    C
    D

  • An element 'X' belongs to the third period and group 16 of the periodic table. Find out the valency of X?

    A
    Valency = 0
    B
    Valency = 2
    C
    Valency = 1
    D
    Valency = 3

    • Similar Questions

    Explore conceptually related problems

    Cl-overset(O)overset(||)C-OC_(2)H_(5)overset((1)'X'RMgX)underset(NH_(4)Cl)rarr3^(@) Alcohol. Find out value of 'X'.

    Demand function of the good X is D_(X)=60-10P . Find out the price of X when demand will be: (i) 20 units (ii) 10 units (iii) 0 units.

    In Fig.80, line A C l in e\ D E\ a n d\ /_A B D=32^0dot Find out the angles x\ a n d\ y\ if /_E=122^0dot

    A set of 'n' identical resistors, each of resistance 'R' when connected in series have an effective resistance 'X'. When they are connected in parallel, their effective becomes 'Y'. Find out the product of X and Y.

    How to find out minimum and maximum values of x and f(x) if f(x)=ax^(2)+bx+c

    Home
    Profile