Home
Class 9
MATHS
ABCD is a quadrilateral in which P, Q, R...

ABCD is a quadrilateral in which P, Q, R and S are mid- points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
`SRabsAC` and `SR=1/2AC`

Answer

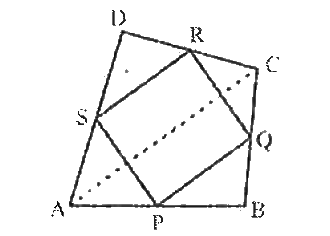
Step by step text solution for ABCD is a quadrilateral in which P, Q, R and S are mid- points of the sides AB, BC, CD and DA. AC is a diagonal. Show that : SRabsAC and SR=1/2AC by MATHS experts to help you in doubts & scoring excellent marks in Class 9 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • QUADRILATERALS

    SUBHASH PUBLICATION|Exercise EXERCISE 7.2|10 Videos

  • PROBABILITY

    SUBHASH PUBLICATION|Exercise EXERCISE 15.1|23 Videos

  • STATISTICS

    SUBHASH PUBLICATION|Exercise EXERCISE 14.3|16 Videos

Similar Questions

Explore conceptually related problems

ABCD is a quadrilateral in which P, Q, R and S are mid- points of the sides AB, BC, CD and DA. AC is a diagonal. Show that : PQ=SR

ABCD is a quadrilateral in which P,Q,R and S are mid points of the sides AB,BC,CD and DA. AC is a diagonal Show that: SR||AC and SR=1/2 AC PQ=SR PQRS is a parallelogram

ABCD is a quadrilateral in which P, Q, R and S are mid- points of the sides AB, BC, CD and DA. AC is a diagonal. Show that : PQRS is a parallelogram.

ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

ABCD is a rectangle and P,Q,R and S are the mid points of the sides AB,BC,CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

ABCD is a rhombus and P,Q,R and S are the mid points of the sides AB,BC,CD and DA. Show that the quadrilateral PQRS is a rectangle.

ABCD is quadrilateral E, F, G and H are the midpoints of AB, BC, CD and DA respectively. Prove that EFGH is a parallelogram.

ABCD is a convex quadrilateral and 3, 4, 5, and 6 points are marked on the sides AB, BC, CD, and DA, respectively. The number of triangles with vertices on different sides is

D is a point on side BC ΔABC such that AD = AC (see figure). Show that AB > AD.

ABCD is a square. E, F, G and H are the mid points of AB, BC, CD and DA respectively. Such that AE = BF = CG = DH . Prove that EFGH is a square.

Home
Profile