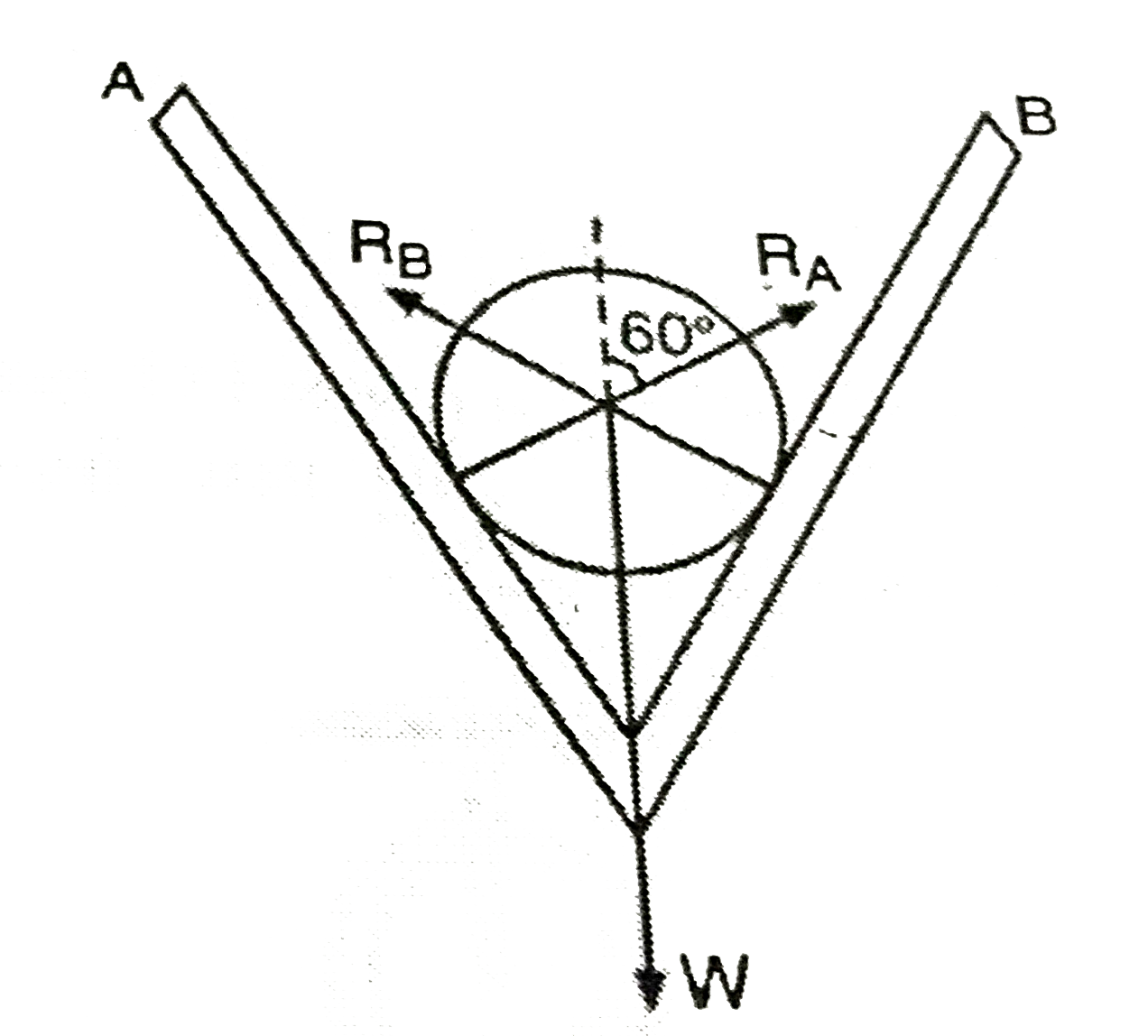Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
FORCE AND NEWTONS LAWS OF MOTION
GRB PUBLICATION|Exercise Objective Questions|134 VideosFORCE AND NEWTONS LAWS OF MOTION
GRB PUBLICATION|Exercise More than one choice is correct|15 VideosFORCE AND NEWTONS LAWS OF MOTION
GRB PUBLICATION|Exercise Problem|33 VideosBASIC MATHEMATICS
GRB PUBLICATION|Exercise Problems For Practice|35 VideosFRICTION AND CIRCULAR MOTION
GRB PUBLICATION|Exercise Comprehension type|11 Videos
Similar Questions
Explore conceptually related problems
GRB PUBLICATION-FORCE AND NEWTONS LAWS OF MOTION-Problem for practice
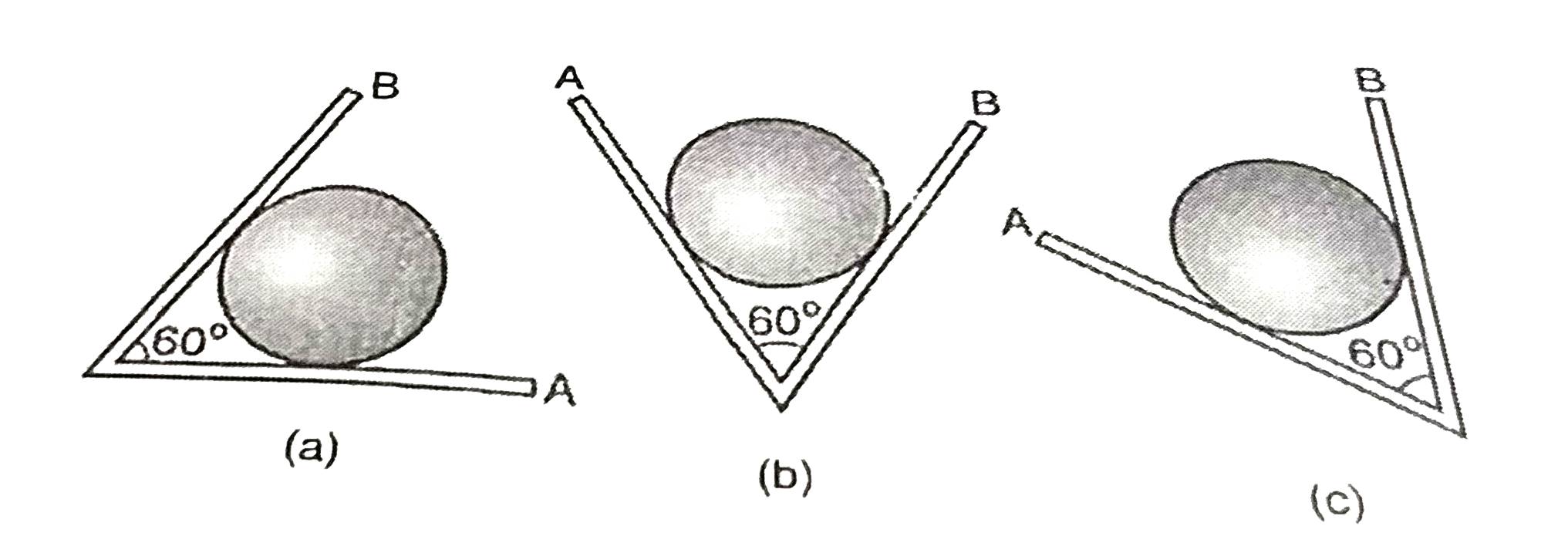
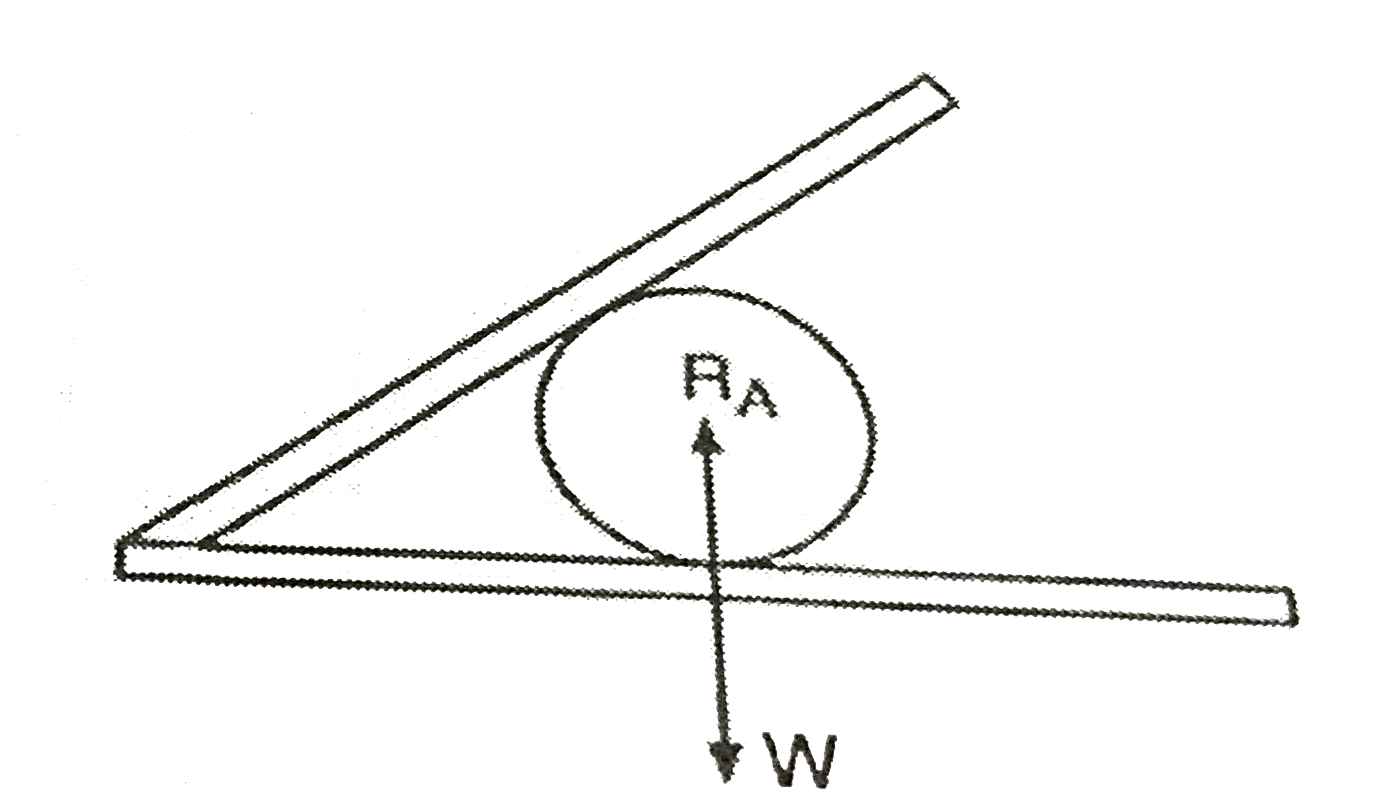
- An iron sphere weights 10 N and rests in a V- shaped trough whose side...
Text Solution
|
- Three blocks of masses m(1)=2kg m(2)=3kg and m(3)=4 kg are in contact ...
Text Solution
|
- A string is wrapped around a log of wood and it is pulled with a force...
Text Solution
|
- Three blocks are connected by strings as shown in and are pulled by a ...
Text Solution
|
- A block of mass M is pulled along a horizontal frictionless surface by...
Text Solution
|
- A block of mass 2 kg is kept at rest on a smooth inclied plane as show...
Text Solution
|
- A light rope fixed to a peg on the ground passes over a tree branch an...
Text Solution
|
- A trolley A has a simple pendulum suspended from a frame fixed to its ...
Text Solution
|
- What force F must be applied so that m(1) and m(2) are at rest on m(3)...
Text Solution
|
- A unifrom flexible chain of length L with weight lambda per unit lengt...
Text Solution
|
- Calculate the tension in the string shown in (a) The pulleys and the...
Text Solution
|
- A block A of mass m is tied to a fixed point C on a horizontal table t...
Text Solution
|
- shows a man of mass 60 kg standing on a light weighing machine kept in...
Text Solution
|
- The systems shown in are in equilibrium if the spring balance is calib...
Text Solution
|
- What is the reading of the spring balance in the following device?
Text Solution
|
- 2 kg box rests on a frictionless of angle 30^(@) supported by a spring...
Text Solution
|
- From three identical springs (each having force constant k) using all ...
Text Solution
|
- Consider the situations shown in fig (a) and (b) initially the spring ...
Text Solution
|
- Two identical blocks, each of mass m, are connected through a massless...
Text Solution
|
- Masses m(1), m(2), m(3) and m(4) are arranged in a system as shown in ...
Text Solution
|