Text Solution
Verified by Experts
|
Topper's Solved these Questions
10 ROTATIONAL
MOTION|Exercise Example 31|1 VideosView Playlist10 ROTATIONAL
MOTION|Exercise Exercise - 1|77 VideosView PlaylistALTERNATING CURRENT
MOTION|Exercise EXERCISE - 4 (LEVEL - II)|14 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
MOTION-10 ROTATIONAL-Exercise - 4 (Level - II)
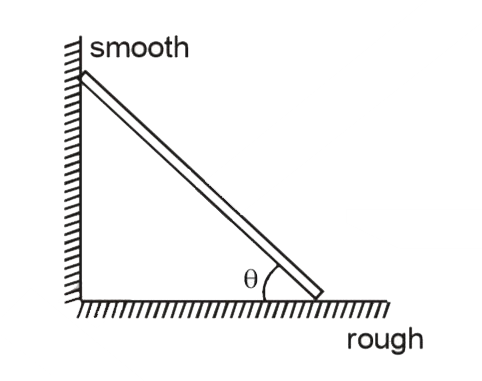
- A stationary uniform rod of mass 'm', length 'l' leans against a smoo...
04:07
|
Playing Now - A block of mass m is held fixed against a wall by a applying a horizon...
01:34
|
Play - A disc has mass 9 m. A hole of radius R/3 is cut from it as shown in t...
03:13
|
Play - A particle moves in circular path with decreasing speed. Which of the ...
01:01
|
Play - A wooden log of mass M and length L is hinged by a frictionless nail a...
02:51
|
Play - A cylinder of mass m and radius R rolls down an inclined plane of incl...
02:09
|
Play - Two identical ladders, each of mass M and length L are resting on the ...
08:17
|
Play - A solid sphere of mass M, radius R and having moment of inertia about ...
01:40
|
Play - A solid cylinder of mass m and radius r is rolling on a rough inclined...
01:13
|
Play - A ball moves over a fixed track as shown in the figure. From A to B ba...
02:34
|
Play - A rectangular plate of mass M and dimension axxb is held in horizonta...
03:55
|
Play - Two discs A and B are mounted coaxially ona vertical axle. The discs h...
01:46
|
Play - Two discs A and B are mounted coaxially ona vertical axle. The discs h...
04:52
|
Play - Two discs A and B are mounted coaxially ona vertical axle. The discs h...
04:52
|
Play - A small object of uniform density rolls up a curved surface with an in...
01:13
|
Play - Satement-1: if there is no external torque on a body about its centre ...
03:04
|
Play - Two cylinders, one hollow (metal) and the other solid (wood) with the ...
02:51
|
Play - A uniform thin cylindrical disk of mass M and radius R is attaached to...
04:44
|
Play - A uniform thin cylindrical disk of mass M and radius R is attaached to...
01:33
|
Play - A uniform thin cylindrical disk of mass M and radius R is attaached to...
03:03
|
Play - If the resultant of all the external forces acting on a system of part...
02:56
|
Play