Home
Class 12
PHYSICS
In the given circuit the capacitor (C) m...

In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch `(S_1)`. Also when `(S_1)` is opend and `(S_2)` is closed the capacitor is connected in series with inductor (L).

At the start, the capicitor was uncharged. when switch `(S_1)` is closed and `(S_2)` is kept open, the time constant of this circuit is `tau`. which of the following is correct

A

after time interval `tau`, charge on the capacitor is CV/2

B

after time interval `2tau`, charge on the capacitor is `CV(1–e^(2))`

C

the work done by the voltage source will be half of the heat dissipated when the capacitor is fully charged.

D

after time interval 2`tau`, charge on the capacitor is `CV(1-e^(-1))`

Text Solution

Verified by Experts

The correct Answer is:
B
Promotional Banner

Topper's Solved these Questions

  • ALTERNATING CURRENT

    MOTION|Exercise EXERCISE - 4 (LEVEL - I)|18 Videos

  • 10 ROTATIONAL

    MOTION|Exercise Exercise - 4 (Level - II)|49 Videos

  • ATOMIC STRUCTURE & X-RAY

    MOTION|Exercise Exercise - 2|31 Videos

Similar Questions

Explore conceptually related problems

In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S_1) . Also when (S_1) is opend and (S_2) is closed the capacitor is connected in series with inductor (L). When the capacitor gets charged compleely, (= (S_1) is opened and (S_2) is closed, Then,

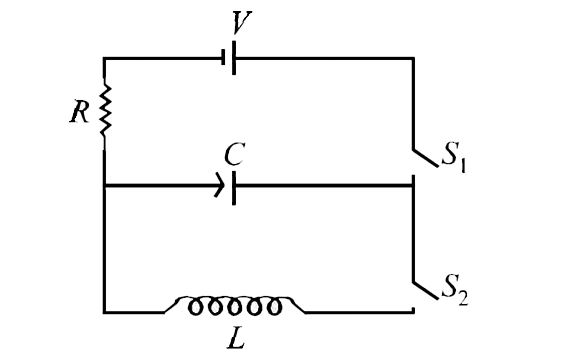
In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S_1) . Also when (S_1) is opend and (S_2) is closed the capacitor is connected in series with inductor (L). Given taht the total charge stored in the LC circuit is (Q_0) . for Tge0, the charge on the capacitor is

The capacitor of capacitance C can be charged (with the help of a resistance R ) by a voltage source V, by closing switch S_(1) while keeping switch S_(2) open. The capacitor can be connected in series with an inductor 'L' by closing switch S_(2) and opening S_(1) . Initially, the capacitor was uncharged. Now , switch S_(1) is closed and S_(2) is kept open. if time constant of this circuit is tau , then

In the circuit shown above, when then switch S is closed,

The capacitor of capacitance C can be charged (with the help of a resistance R) by a voltage source V, by closing switch S_1 while keeping switch S_2 open. The capacitor can be connected in series with an inductor ‘L’ by closing switch S_2 and opening S_1 After the capacitor gets fully charged, S_1 is opened and S_2 is closed so that the inductor is connected in series with the capacitor. Then,

In the circuit shown, all the capacitors are initially uncharged. The current through the battery just after closing the switch 'S' is