Text Solution
Verified by Experts
Topper's Solved these Questions
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
NCERT EXEMPLAR|Exercise very short answer type questions|18 VideosSYSTEM OF PARTICLES AND ROTATIONAL MOTION
NCERT EXEMPLAR|Exercise very short answer type questions|18 VideosOSCILLATIONS
NCERT EXEMPLAR|Exercise MULTIPLE CHOICE QUESTIONS (MCQs)|40 VideosTHERMAL PROPERTIES OF MATTER
NCERT EXEMPLAR|Exercise Very short Answer type Questions|15 Videos
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-SYSTEM OF PARTICLES AND ROTATIONAL MOTION -Long answer type questions
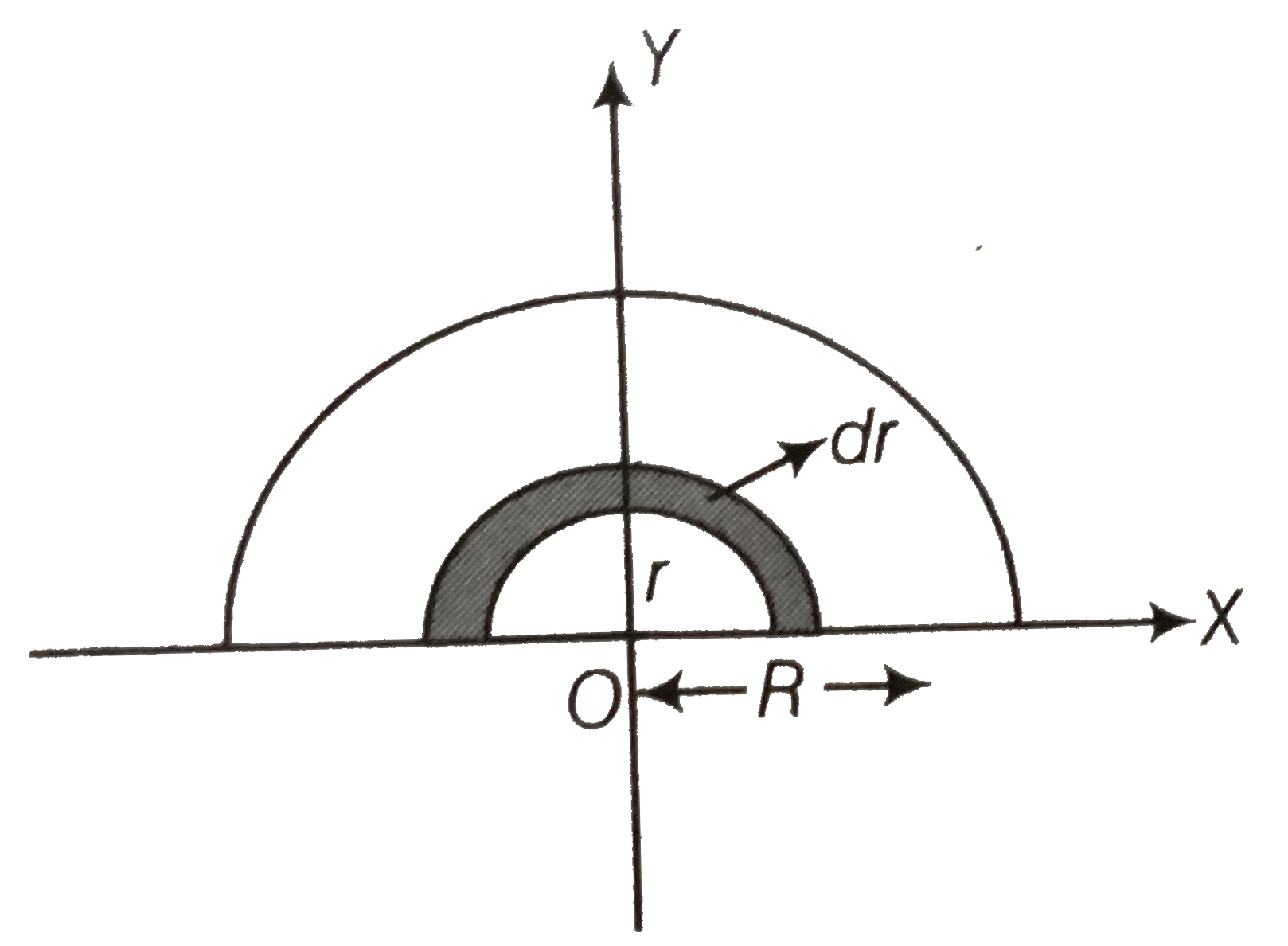
- Find the centre of mass of a unifrom (a) half-disc,(b) quarter-disc.
Text Solution
|
- Two discs of moments of inertia I(1) and I(2) about their respective a...
Text Solution
|
- A disc of radius R is rotating with an angular speed omega(0) about a ...
Text Solution
|
- Two cylindrical hollow drums of radii R and 2R, and of a commom height...
Text Solution
|
- A uniform square plate S (side c) and a unifrom rectangular plate R(si...
Text Solution
|
- A unifrom disc of radius R, is resting on a table on its rim. The coef...
Text Solution
|
- Find the centre of mass of a uniform : (a) half-disc, (b) quarter-di...
Text Solution
|
- Two discs of moments of inertia I(1) " and" I(2) about their respectiv...
Text Solution
|
- A disc of radius R is rotating with an angular speed omega(0) about a ...
Text Solution
|
- Two cylindrical hollow drums of radii R and 2R, and of a commom height...
Text Solution
|
- A uniform square plate S (side c) and a unifrom rectangular plate R(si...
Text Solution
|
- A unifrom disc of radius R, is resting on a table on its rim. The coef...
Text Solution
|