Text Solution
Verified by Experts
NCERT EXEMPLAR-MOTION IN A PLANE-Multiple Choice Questions
- A ball is thrown from a roof top at angle of 40^(@)above the horizont...
Text Solution
|
- A football is kicked into the air vertically upwards. What is its (a) ...
Text Solution
|
- vec A , vec B and vec C are three non-collinear, non co-planar vectors...
Text Solution
|
- A boy travelling in an open car moving on a levelled road with constan...
Text Solution
|
- A boy throws a ball in air at 60^@ to the horizontal along a road wit...
Text Solution
|
- In dealing with motion of projectile in air, we ignore effect of air r...
Text Solution
|
- A fighter plane is flying horizontally at an altitude of 1.5 km with s...
Text Solution
|
- (a) Earth can be thought of as a sphere of radius 64 00 km. Any objec...
Text Solution
|
- Given below in Column I are the relations between vectors a,b and c an...
Text Solution
|
- If |A|=2 and |B| = 4, then match the relation in Column I with the ang...
Text Solution
|
- If | vec A | =2 and | vec B| =4, then match the relations in column ...
Text Solution
|
- A hill is 500 m high. Supplies are to be across the hill using a cano...
Text Solution
|
- A gun can fire shells with maximum speed v(0) and the maximum horizont...
Text Solution
|
- A particle is projected in aer an angle beta to a surface which itsel...
Text Solution
|
- A particle falling vertically from a height hits a plane surface incli...
Text Solution
|
- A girl riding a bicycle with a speed of 5 m//s to wards Noth directio...
Text Solution
|
- A river is flowing due east with a speed 3 m//s (Fig. 2 (EP) .31 ). ...
Text Solution
|
- A cricket fielder can throw the cricket ball with a speed v0. If he t...
Text Solution
|
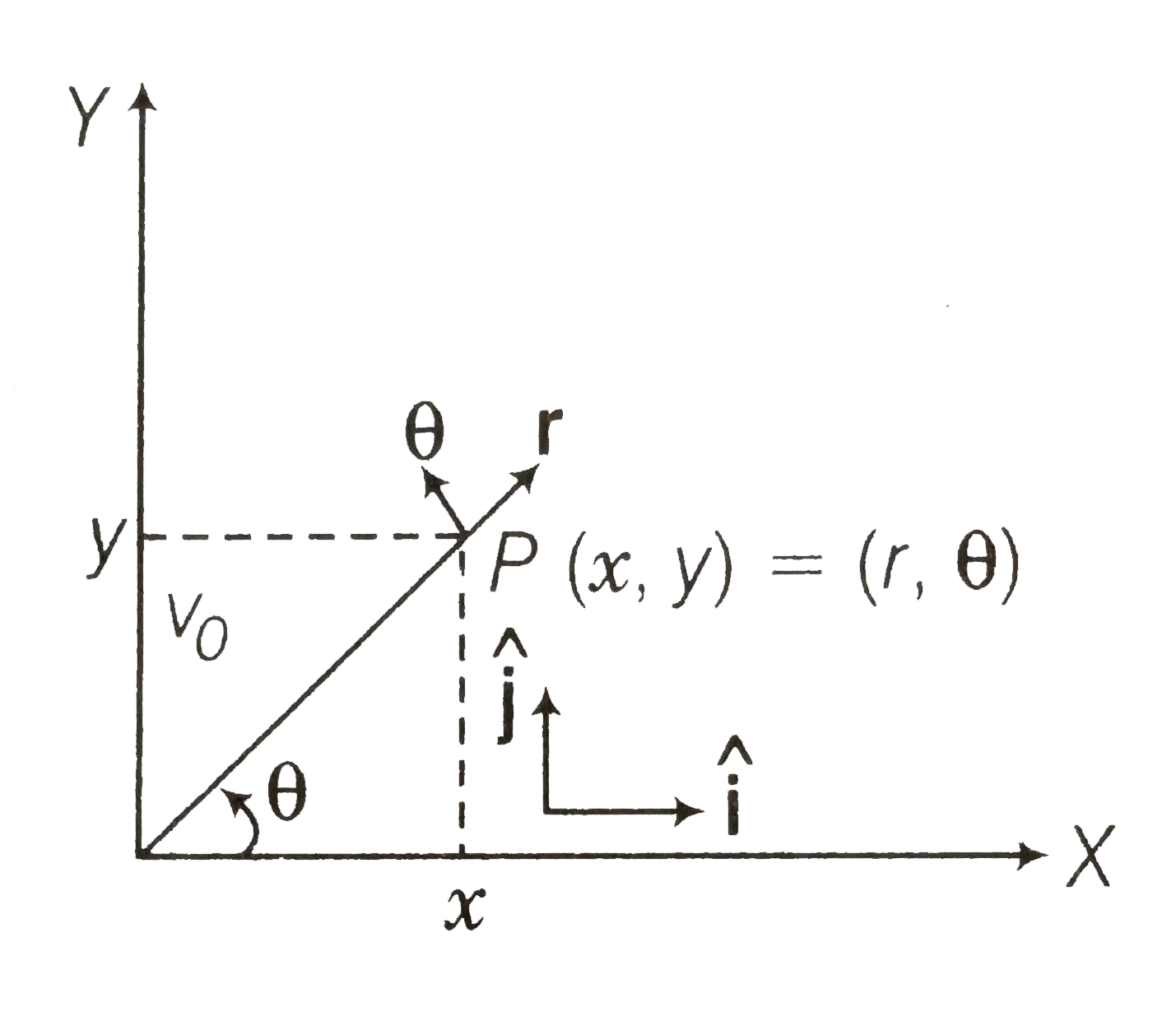
- Motion in two dimensions, in a plane can be studied by expressing posi...
Text Solution
|
- A man wants to reach from A to the opposite corner of the square C. T...
Text Solution
|