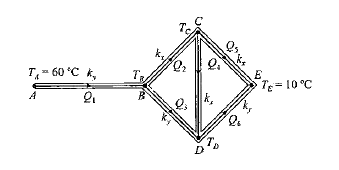
Text Solution
Verified by Experts
Topper's Solved these Questions
HEAT TRANSFER
PHYSICS GALAXY - ASHISH ARORA|Exercise Illustrative Example 4.18|1 VideosHEAT TRANSFER
PHYSICS GALAXY - ASHISH ARORA|Exercise Illustrative Example 4.19|1 VideosHEAT TRANSFER
PHYSICS GALAXY - ASHISH ARORA|Exercise Illustrative Example 4.16|1 VideosHEAT AND THERMAL EXPANSION
PHYSICS GALAXY - ASHISH ARORA|Exercise UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO|82 VideosKinetic Theory of Gases and Gas Laws
PHYSICS GALAXY - ASHISH ARORA|Exercise Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO|64 Videos
Similar Questions
Explore conceptually related problems