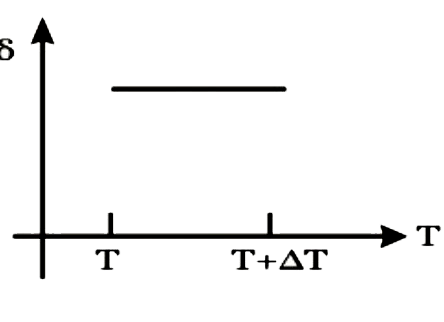
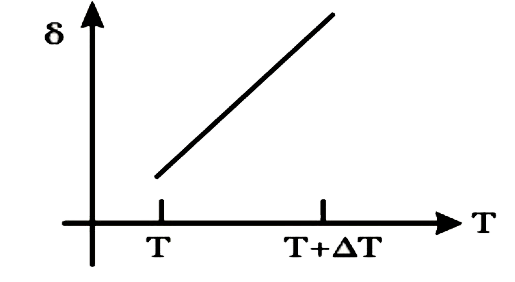
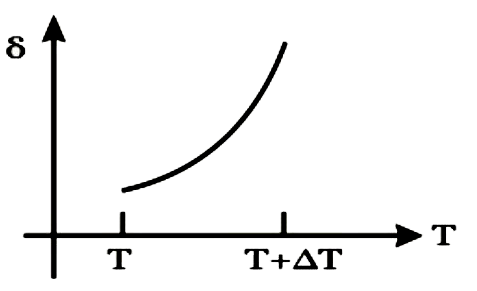
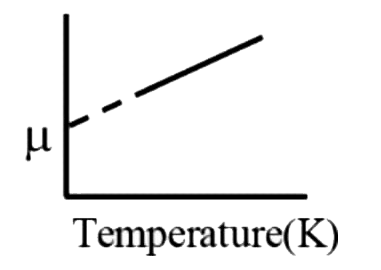
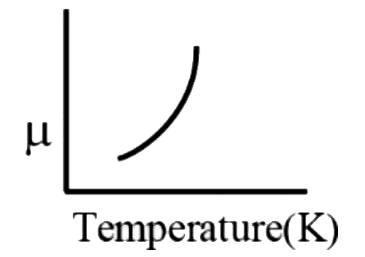
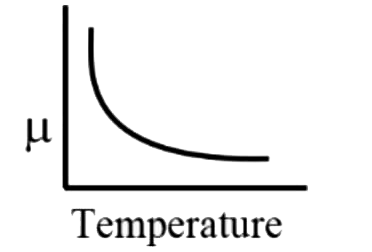
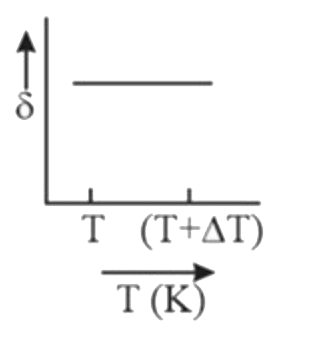
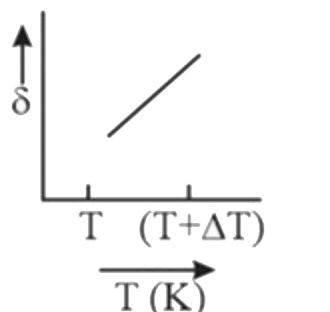
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
NTA NEET SET 52
NTA MOCK TESTS|Exercise PHYSICS|45 VideosView PlaylistNTA NEET SET 54
NTA MOCK TESTS|Exercise PHYSICS|44 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
NTA MOCK TESTS-NTA NEET SET 53-PHYSICS
- The temperature of sun is 5500 K and it emits maximum intensity radiat...
01:50
|
Play - The variation of photocurrent with collector potential for different f...
07:58
|
Play - An ideal gas is initially at temperature T and volume V . Its volume i...
03:34
|
Playing Now - A gas can be taken from A to B via two different processes ACB and DB...
02:33
|
Play - A truck of mass 10 metric ton runs at 3ms^(-1) along a level track and...
04:13
|
Play - A thin flexible wire of length L is connected to two adjacent fixed po...
06:29
|
Play - A one mole of an ideal gas expands adiabatically at constant pressure...
02:38
|
Play - A cylindrical conductor of diameter 0.1 mm carries a current of 90 ma....
02:30
|
Play - In an AC circuit , current is 3A and voltage 210V and power is 63W. Th...
01:04
|
Play - The upper half of an inclined plane with inclination phi is perfectly ...
05:20
|
Play - The potential energy for a conservative force system is given by U=ax^...
01:48
|
Play - Starting with a sample of pure .^(66)Cu, 7//8 of it decays into Zn in ...
01:12
|
Play - The ends of a rod of length l and mass m are attached to two identica...
14:22
|
Play - A pendulum is executing simple harmonic motion and its maximum kinet...
07:45
|
Play - A photocell is illuminated by a small bright source places 1 m away w...
01:36
|
Play - The magnitude of x and y components of vec(A) are 7 and 6 respectively...
02:06
|
Play - The work done in blowing a bubble of volume V is W, then what is the w...
02:56
|
Play - A body is projected at time t = 0 from a certain point on a planet's s...
01:03
|
Play - A body of mass 8 kg is suspended through two light springs X and Y con...
01:46
|
Play - The two surfaces of a biconvex lens has same radii of curvatures . Thi...
08:58
|
Play