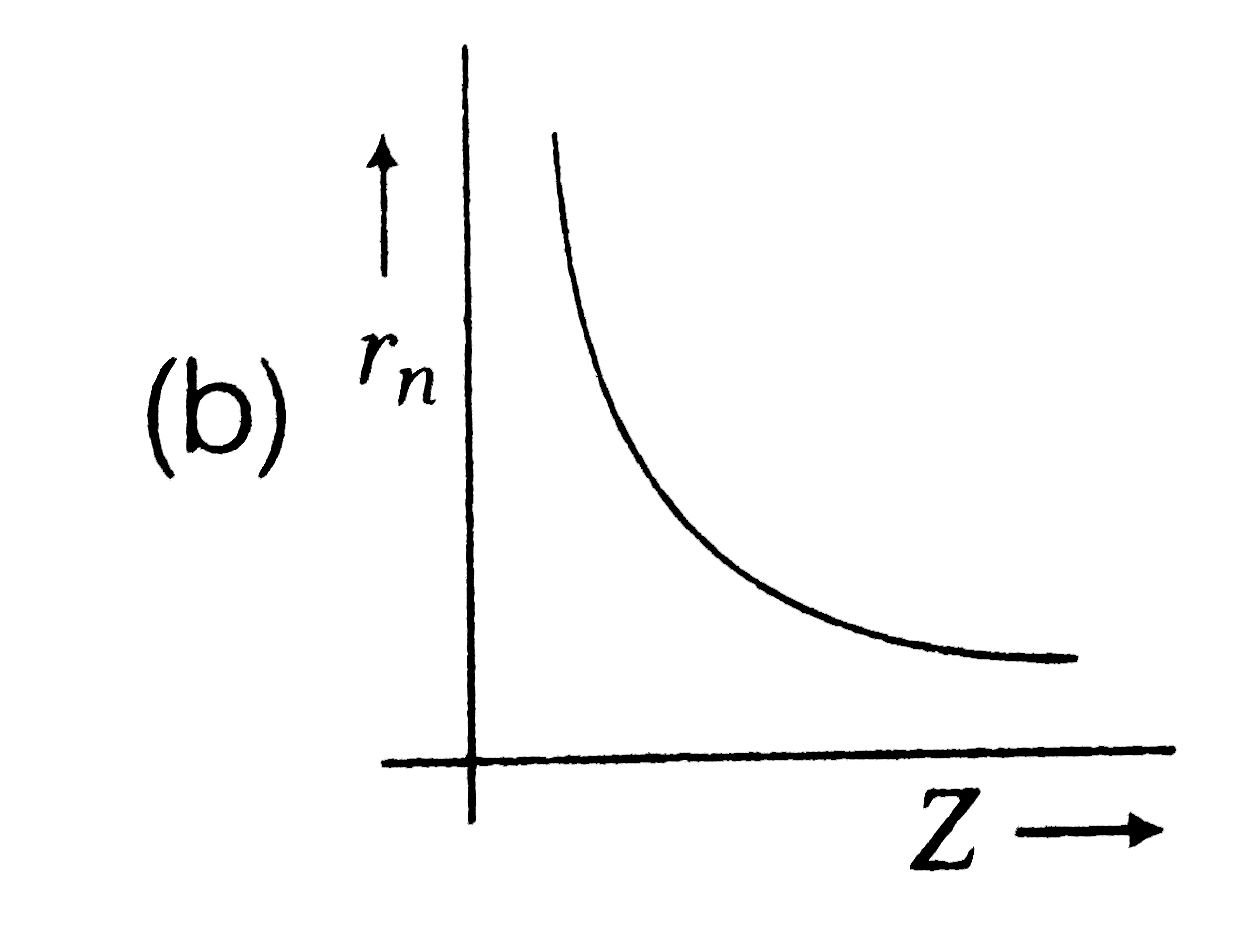
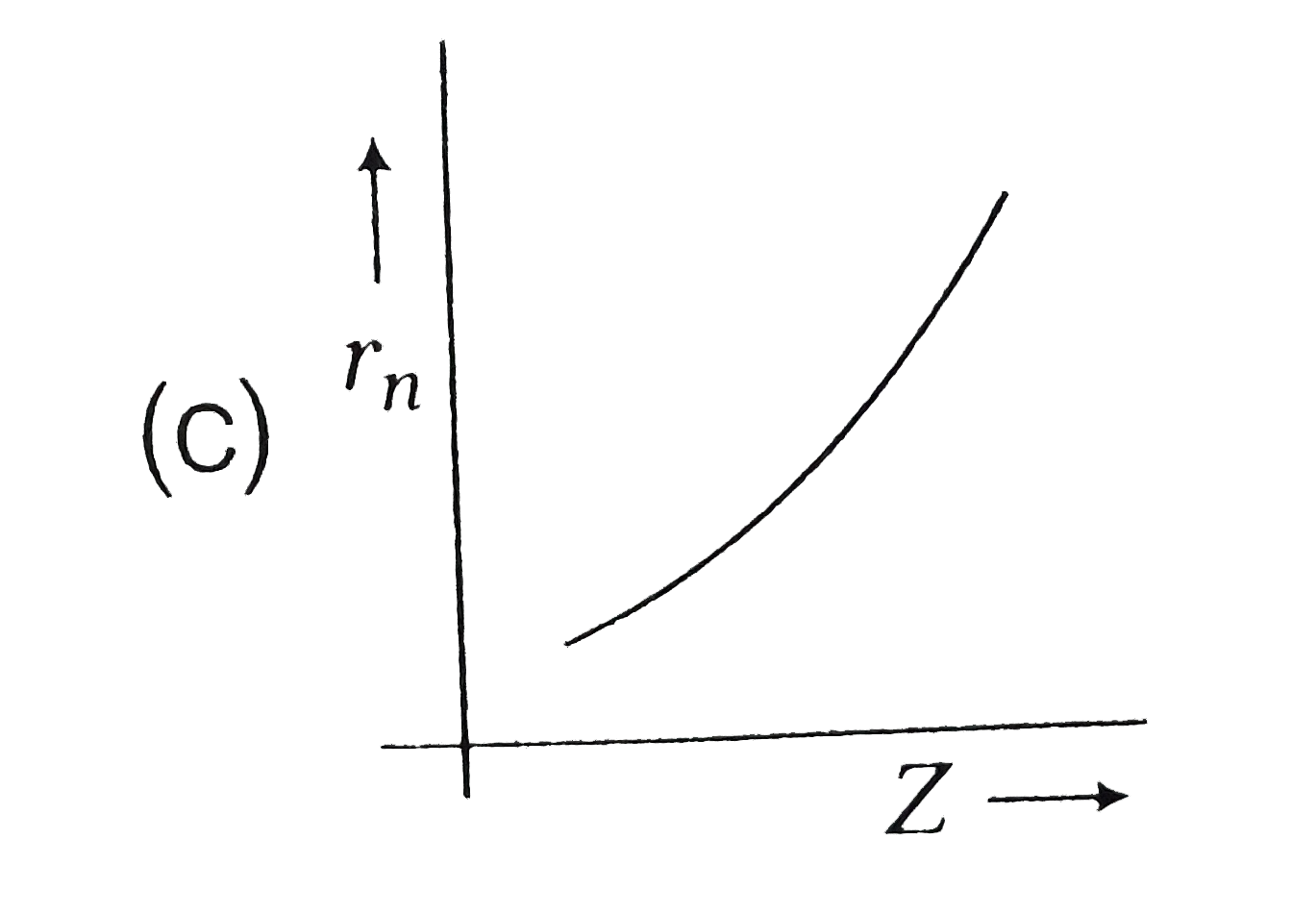
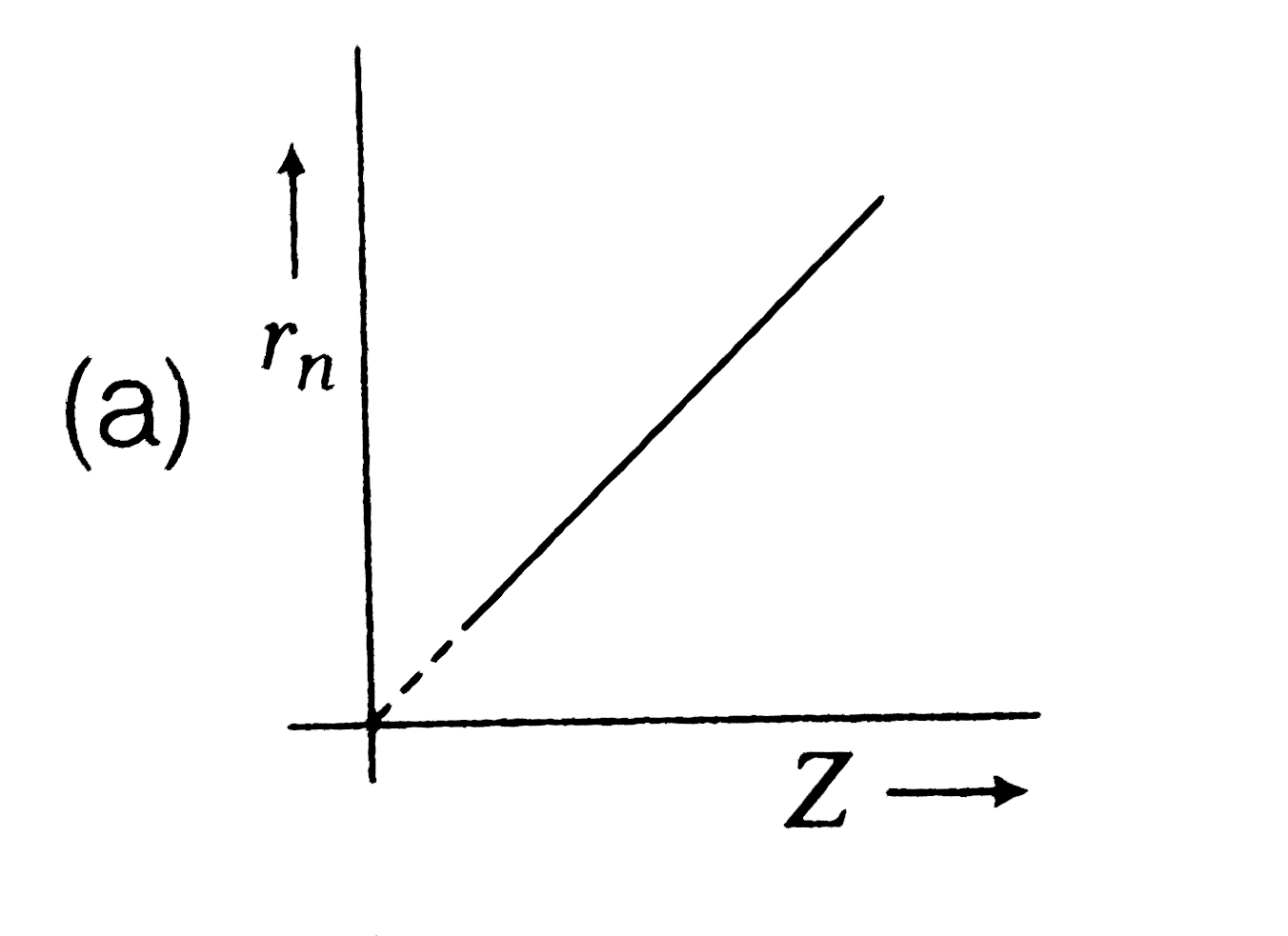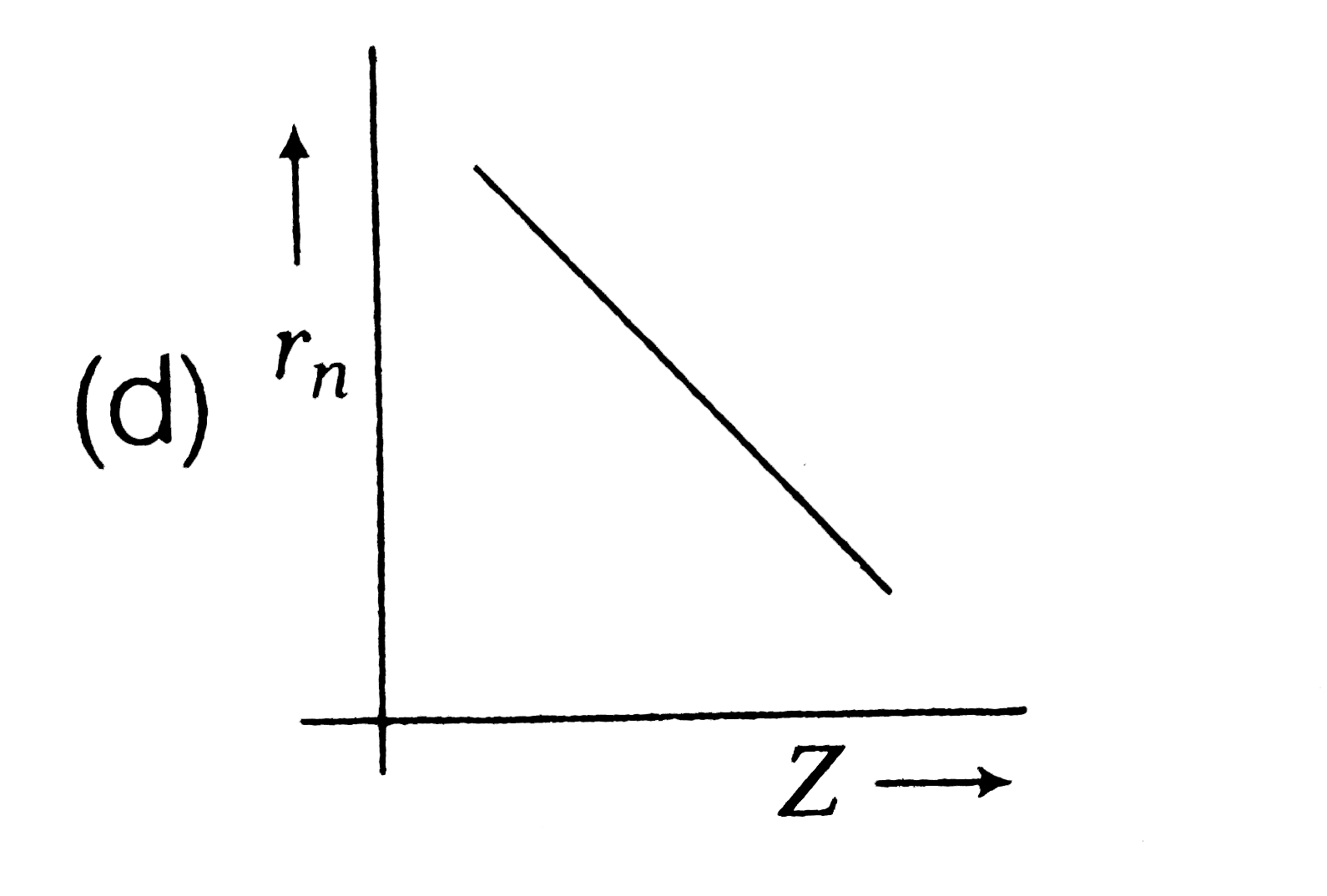A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
ATOMS
DC PANDEY|Exercise Check point 12.2|16 VideosView PlaylistATOMS
DC PANDEY|Exercise Check point 12.3|15 VideosView PlaylistATOMS
DC PANDEY|Exercise MEDICAL ENTRANCES GALLERY|42 VideosView PlaylistALTERNATING CURRENT
DC PANDEY|Exercise JEE MAIN|63 VideosView PlaylistCAPACITORS
DC PANDEY|Exercise OBJECTIVE_TYPE|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
DC PANDEY-ATOMS-Check point 12.1
- The radius of the atom is of the order of
01:54
|
Play - According to classical theory, the circular path of an electron in Rut...
01:12
|
Play - An alpha nucleus of energy (1)/(2)m nu^(2) bombards a heavy nucleus o...
04:31
|
Play - The number of alpha-particless scattered per unit area N (theta) at sc...
03:28
|
Play - in Rutherford scattering experiment for scattering angle of 180^(@) , ...
03:00
|
Play - The concept of stationary orbits was proposed by
05:47
|
Play - In Bohr's atom model,
01:58
|
Play - The angular momentum (L) of an electron moving in a stable orbit aroun...
05:36
|
Play - In Bohr's mode, the atomic radius of the first orbit is r(0) then the ...
03:43
|
Play - In which of the following systems will the radius of the first orbit (...
02:07
|
Play - Radius (r(n)) of electron in nth orbit versus atomic number (Z) graph ...
02:20
|
Playing Now - The ratio of the speed of the electrons in the ground state of hydroge...
02:22
|
Play - Speed (V(n)) of electron in nth orbit versus principal quantum number ...
Text Solution
|
Play - The orbital frequency of an electron in the hydrogen atom is proportio...
01:58
|
Play