Text Solution
Verified by Experts
|
Topper's Solved these Questions
WORK, ENERGY AND POWER
FIITJEE|Exercise SOLVED PROBLEMS ( OBJECTIVE)|18 VideosView PlaylistWORK, ENERGY AND POWER
FIITJEE|Exercise SOLVED PROBLEMS ( OBJECTIVE) ASSERTION REASONING TYPE|1 VideosView PlaylistWORK, ENERGY AND POWER
FIITJEE|Exercise COMPREHENSIONS ( Comprehension-II)|5 VideosView PlaylistTEST PAPERS
FIITJEE|Exercise PHYSICS|747 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
FIITJEE-WORK, ENERGY AND POWER -SOLVED PROBLEMS (SUBJECTIVE )
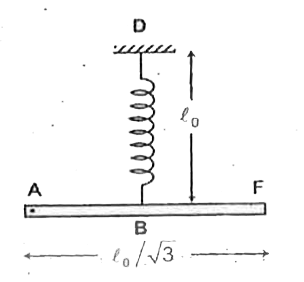
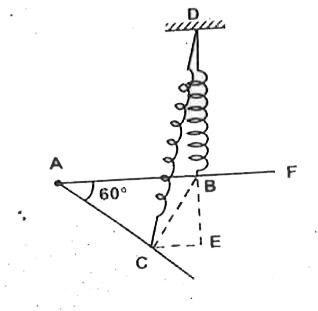
- In the figure shown one end of a light spring of natural length l(0)=s...
14:50
|
Playing Now - Two smooth wedges of equal mass m are placed as shown in figure. All s...
05:37
|
Play - What is the power required to push the woodn wedge horizontally with c...
04:24
|
Play - Two blocks of masses m(1) and m(2) are connected by a spring of stiffn...
05:35
|
Play - A block of mass m moving with a velocity v(0) on a rough horizontal su...
03:36
|
Play - A particle of mass m is attached to the celling of a cabin with an in...
06:13
|
Play - A horizontal plane supports a plank with a bar of mass m=1.0kg placed ...
08:38
|
Play - A small block is projected with a speed v( 0) on a horizontal track pl...
Text Solution
|
Play