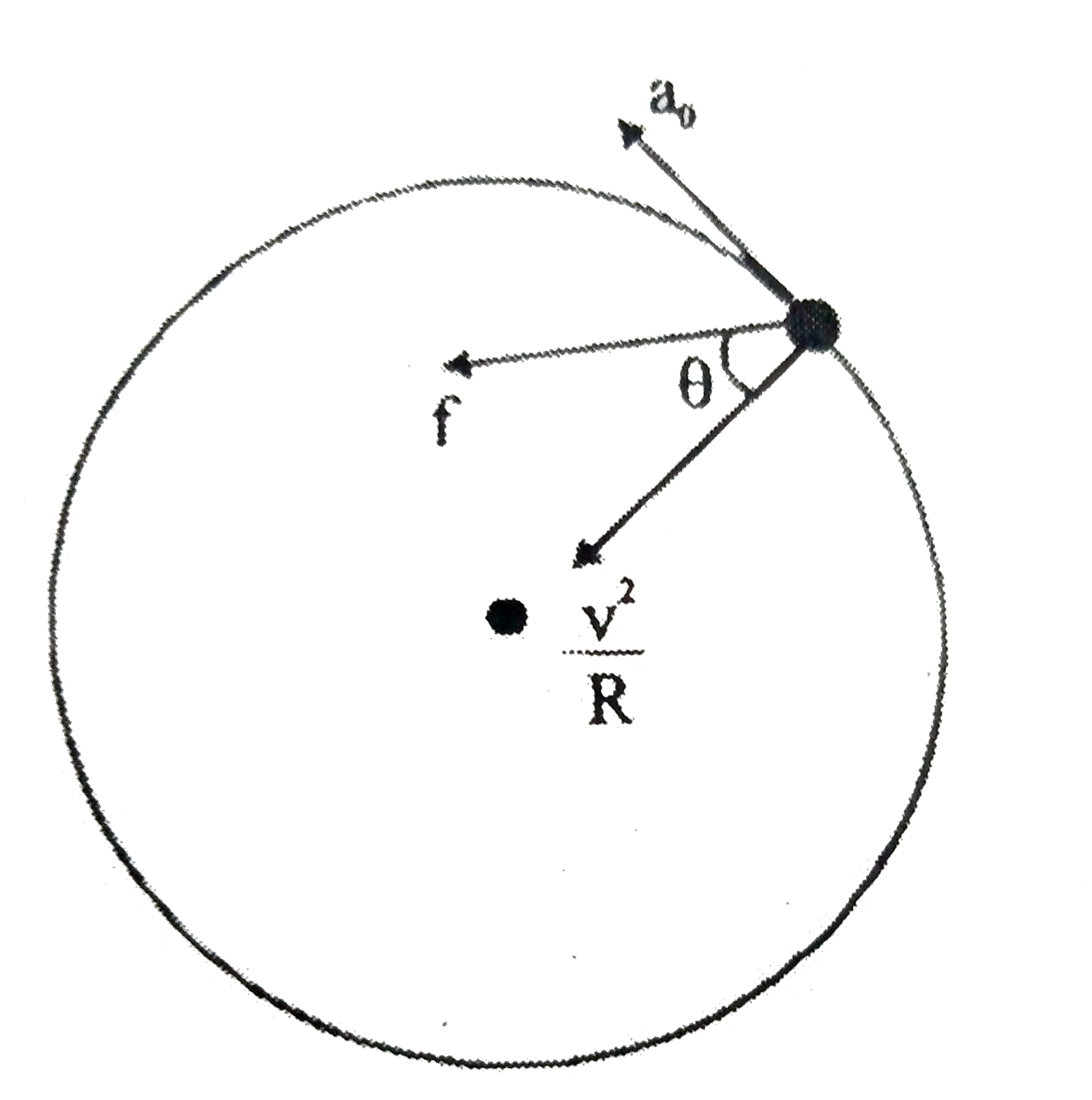
A car starts from rest with a constant t...

A car starts from rest with a constant tangential acceleration `a_(0)` in a circular path of radius r. At time t, the car kids, find the value of coefficient of friction.

Text Solution

Verified by Experts

The tangential and centripetal acceleration is provided only by the frictionless force.
`Thus, f sin theta, fcos theta=(mv^(2))/(r)=(m(a_(0)t)^(2))/(r)`
`Rightarrow f=m sqrt(a_(0)^(2)+((a_(o)t)^(4))/(r^(2)))=ma_(0)sqrt(1+a_(0)^(2)t^(4))/(r_(2))=f_("max")`
`mumg=ma_(0) sqrt(1+(a_(0)^(2)t^(4))/(r^(2))) Rightarrow mu=(a_(0))/(g)sqrt(1+(a_(0)^(2)t^(2))/(r^(2)))`

Topper's Solved these Questions

CIRCULAR MOTION
ALLEN|Exercise EXERCISE (S-1)|10 Videos
CIRCULAR MOTION
ALLEN|Exercise Dynamics of circular motion|8 Videos
BASIC MATHS
ALLEN|Exercise Question|1 Videos
CURRENT ELECTRICITY
ALLEN|Exercise All Questions|427 Videos

A particle starting from rest moves with a constant angular acceleration alpha in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is -

`(1)/(alpha)`

`alpha`

`(1)/(sqrt(alpha))`

`sqrt(alpha)`

A particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is

`1// alpha`

`sqrtalpha`

`1// sqrt alpha`

`alpha`

A car starts moving from rest on a horizontal circular road of radius of curvature R at . The speed of the car is increasing at a constant rate a. The coefficient of friction between the road and the tyres of the car is The car starts slipping at time t = t_(0) . Then t_(0) is equal to:

`(.^(4)sqrt(mu^(2) g^(2) R^(2)))/(a)`

`(.^(4)sqrt(R^(2) (mu^(2) g^(2) - a^(2))))/(a)`

`(.^(4)sqrt(R^(2) (a^(2) - mu^(2) g^(2))))/(a)`

`(.^(4)sqrt(R^(2) (mu^(2) g^(2) + a^(2))))/(a)`