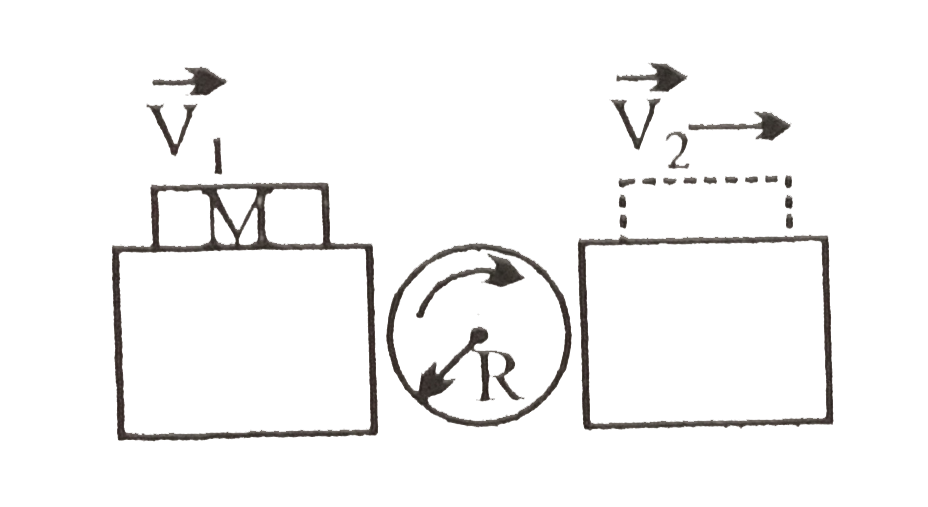
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
TEST PAPERS
BANSAL|Exercise Physics, SECTION-1 (PART-A) [MULTIPLE CORRECT CHOICE TYPE]|5 VideosTEST PAPERS
BANSAL|Exercise Physics, SECTION-1 (PART-B) [MATRIX TYPE]|2 VideosTEST PAPERS
BANSAL|Exercise Physics, SECTION-1 (PART-A)|5 VideosPROBABILITY
BANSAL|Exercise All Questions|1 VideosTHERMODYNAMICS
BANSAL|Exercise Match the column|7 Videos
Similar Questions
Explore conceptually related problems