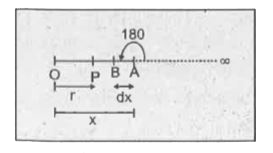
Text Solution
Verified by Experts
Topper's Solved these Questions
MODEL TEST PAPER (SOLVED)
MBD -HARYANA BOARD|Exercise LONG ANSWER TYPE QUESTIONS|6 VideosMODEL TEST PAPER (SOLVED)
MBD -HARYANA BOARD|Exercise VERY SHORT ANSWER TYPE QUESTIONS|10 VideosMAGNETISM
MBD -HARYANA BOARD|Exercise OBJECTIVE TYPE QUESTIONS|17 VideosMODEL TEST PAPER - 2
MBD -HARYANA BOARD|Exercise SET - D ( LONG ANSWER TYPE QUESTIONS)|4 Videos
Similar Questions
Explore conceptually related problems
MBD -HARYANA BOARD-MODEL TEST PAPER (SOLVED)-SHORT ANSWER TYPE QUESTIONS
- Derive the expression for the electric potential due to an electric di...
Text Solution
|
- Derive an experssion for the average power in LCR circuit connected to...
Text Solution
|
- What is total internalreflection ? What is the meaning of critical ang...
Text Solution
|
- State two laws of photoelectric emission. Are cathode rays waves or pa...
Text Solution
|
- What are the postulates of Bohr's model of an atom?
Text Solution
|
- A conductor of length l is connected to a.d.c, source of potential V. ...
Text Solution
|
- Derive a relation between current gain of common emitter amplifier.
Text Solution
|