A
B
C
D
Text Solution
Verified by Experts
|
Topper's Solved these Questions
COLLISION
FIITJEE|Exercise SOLVED PROBLEMS (OBJECTIVE) ASSERTION REASONING TYPE|1 VideosView PlaylistCOLLISION
FIITJEE|Exercise SOLVED PROBLEMS (OBJECTIVE) COMPREHENSION - I|3 VideosView PlaylistCOLLISION
FIITJEE|Exercise SOLVED PROBLEMS (SUBJECTIVE)|10 VideosView PlaylistAC CIRCUITS
FIITJEE|Exercise ASSERTION REASONING TYPE|1 VideosView PlaylistCURRENT ELECTRICITY
FIITJEE|Exercise Comprehension -4|3 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
FIITJEE-COLLISION -SOLVED PROBLEMS (OBJECTIVE)
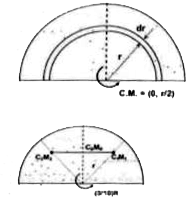
- Find the position of centre of mass of the quarter solid sphere from '...
Text Solution
|
Playing Now - The centre of mass of a, non uniform rod of length L whose mass per un...
03:51
|
Play - A uniform circular disc of mass 2 m and radius R placed freely on a ho...
12:36
|
Play - Internal forces can change
04:01
|
Play - Two blocks of masses 2 kg and 1 kg respectively are tied to the ends o...
08:48
|
Play - A boy of mass 60kg is standing over a platform of mass 40kg placed ove...
05:38
|
Play - A ball moving with a momentum of 5kg ms^(-1) strikes against a wall at...
07:06
|
Play - Five identical balls each of mass m and radius r are string like beads...
04:37
|
Play - A bomb of mass m is thrown with velocity v. It explodes and breaks int...
02:34
|
Play - If the KE of a body becomes four times its initial value, then the new...
03:03
|
Play - A massive ball moving with speed v collieds with a tiny ball which is ...
01:56
|
Play - A bomb traveling in a parabolic path under the effect of gravity, expl...
01:50
|
Play - Sphere A of mass 'm' moving with a constant velocity u hits another st...
03:46
|
Play - A body of mass 1 kg initially at rest, explodes and breaks into three ...
05:06
|
Play - An elastic sphere is dropped from a height of 4 m upon a fixed horizon...
08:05
|
Play - A particle of mass m falls from a height h on a mass m and gets stuck ...
Text Solution
|
Play - In the figure shown
02:00
|
Play - A particle moving with kinetic energy E makes and head on elastic coll...
05:19
|
Play