Text Solution
AI Generated Solution
|
Topper's Solved these Questions
GRAVITATION
MODERN PUBLICATION|Exercise COMPETITION FILE (Integer Types questions)|12 VideosView PlaylistMATHEMATICAL TOOLS
MODERN PUBLICATION|Exercise PRACTICE PROBLEMS (10)|12 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-GRAVITATION-Chapter Practice Test
- The weight of a body at the centre of the earth is
01:20
|
Play - If the diameter and mass of the earth becomes twice becomes twice of i...
02:06
|
Play - What is the unit and dimensional formula of gravitational field intens...
01:39
|
Play - Does the escape velocity of a body depend on the density of a planet ?
01:43
|
Play - A satellite revolving around Earth loses height. How will its time per...
02:40
|
Play - Escape velocity from the surface of moon is less than that from the su...
04:14
|
Play - Distinguish between polar satellites and geostationary satellites.
04:19
|
Play - What are the conditions under which a rocket, fired from the earth, la...
02:08
|
Play - What is binding energy of a satellite?
02:28
|
Play - How will the acceleration due to gravity will change if the radius ea...
03:54
|
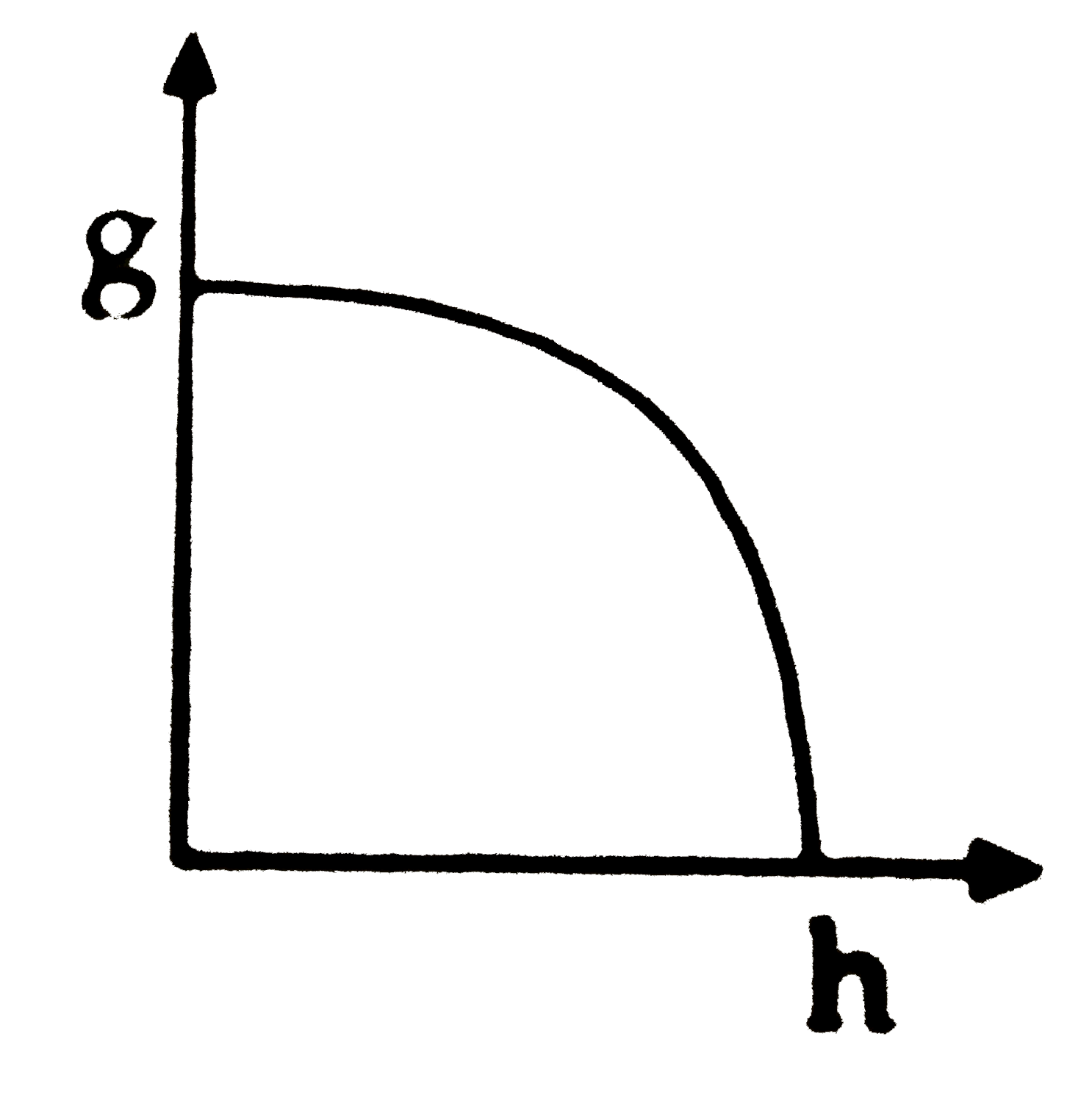
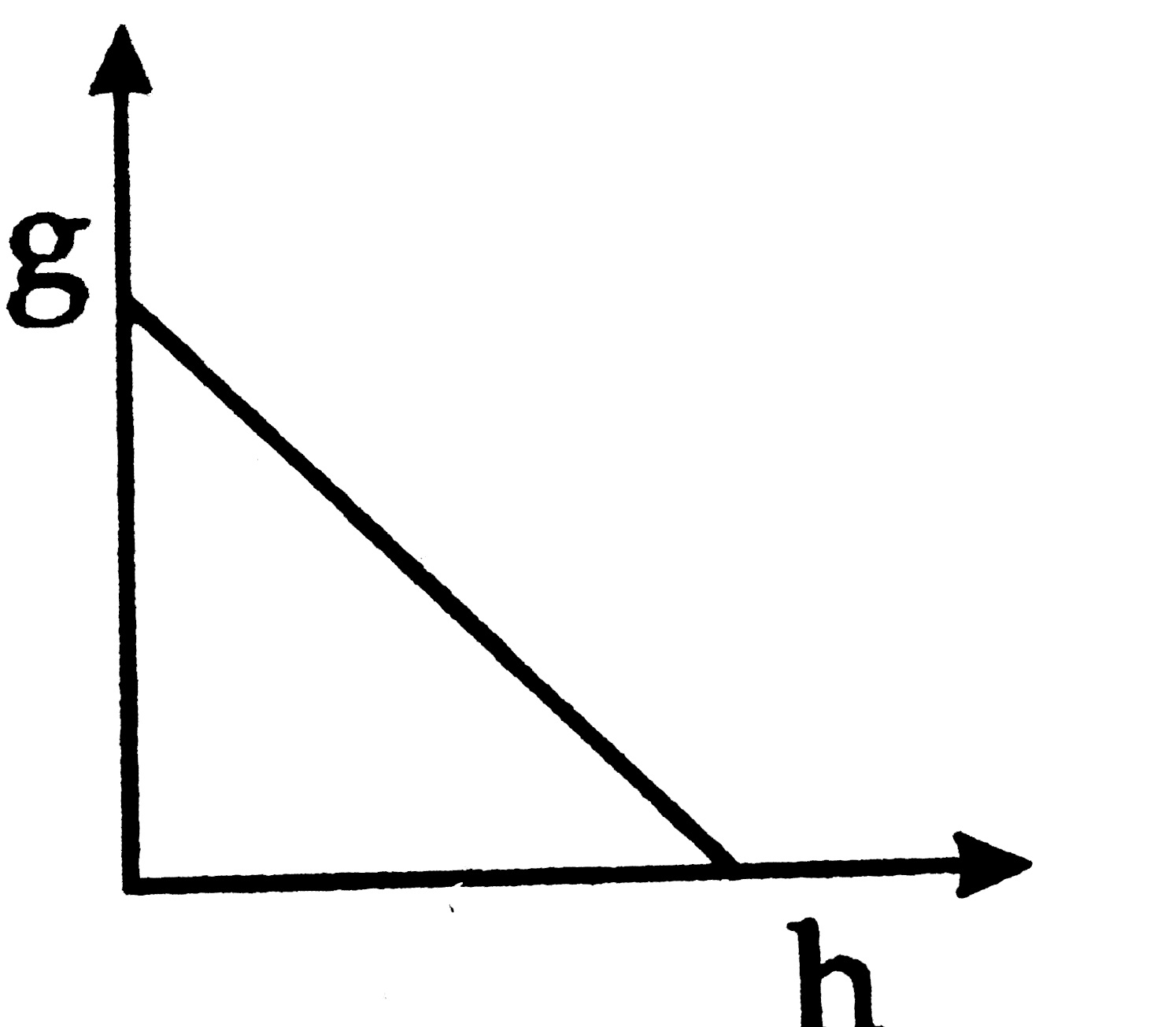
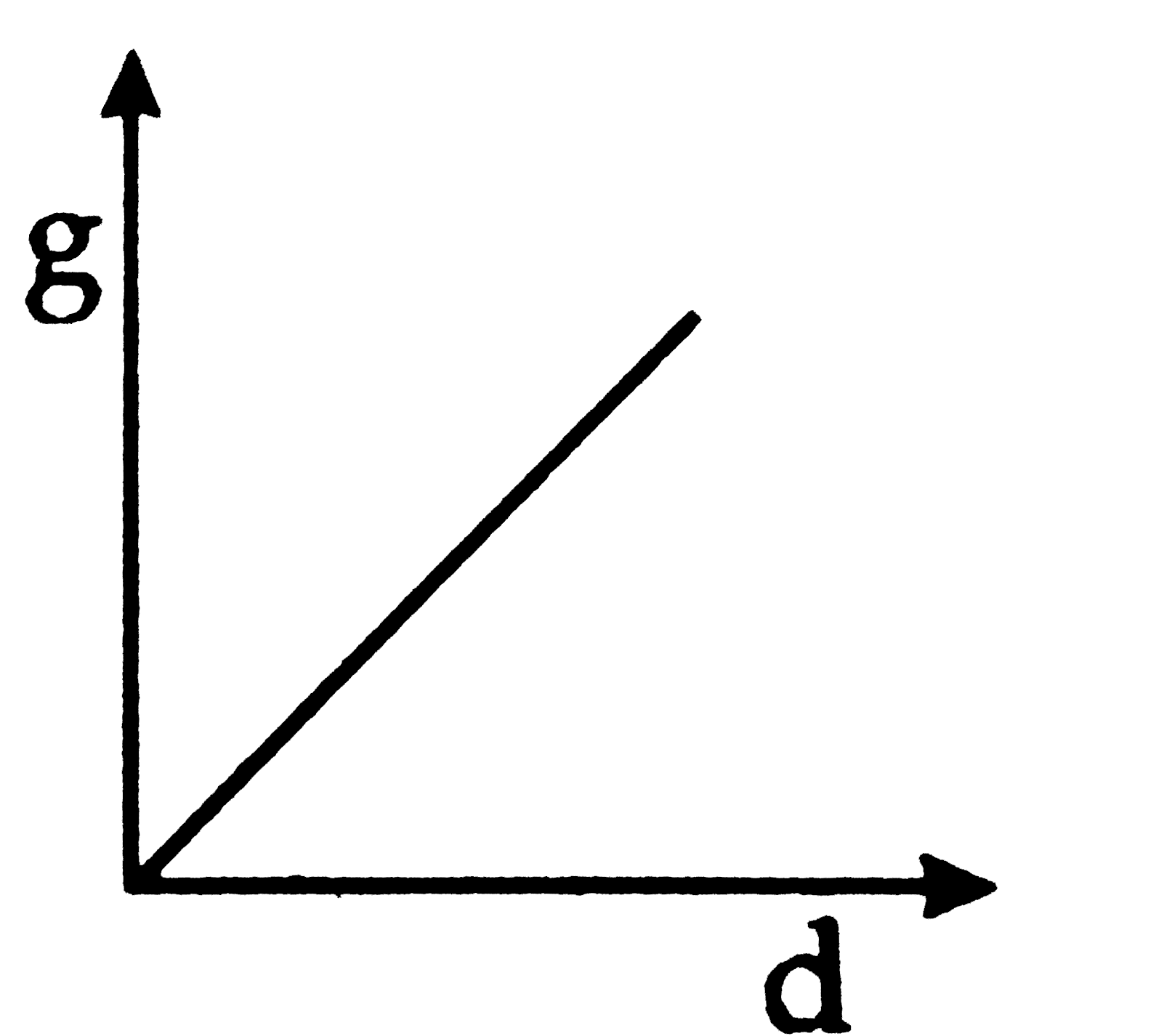
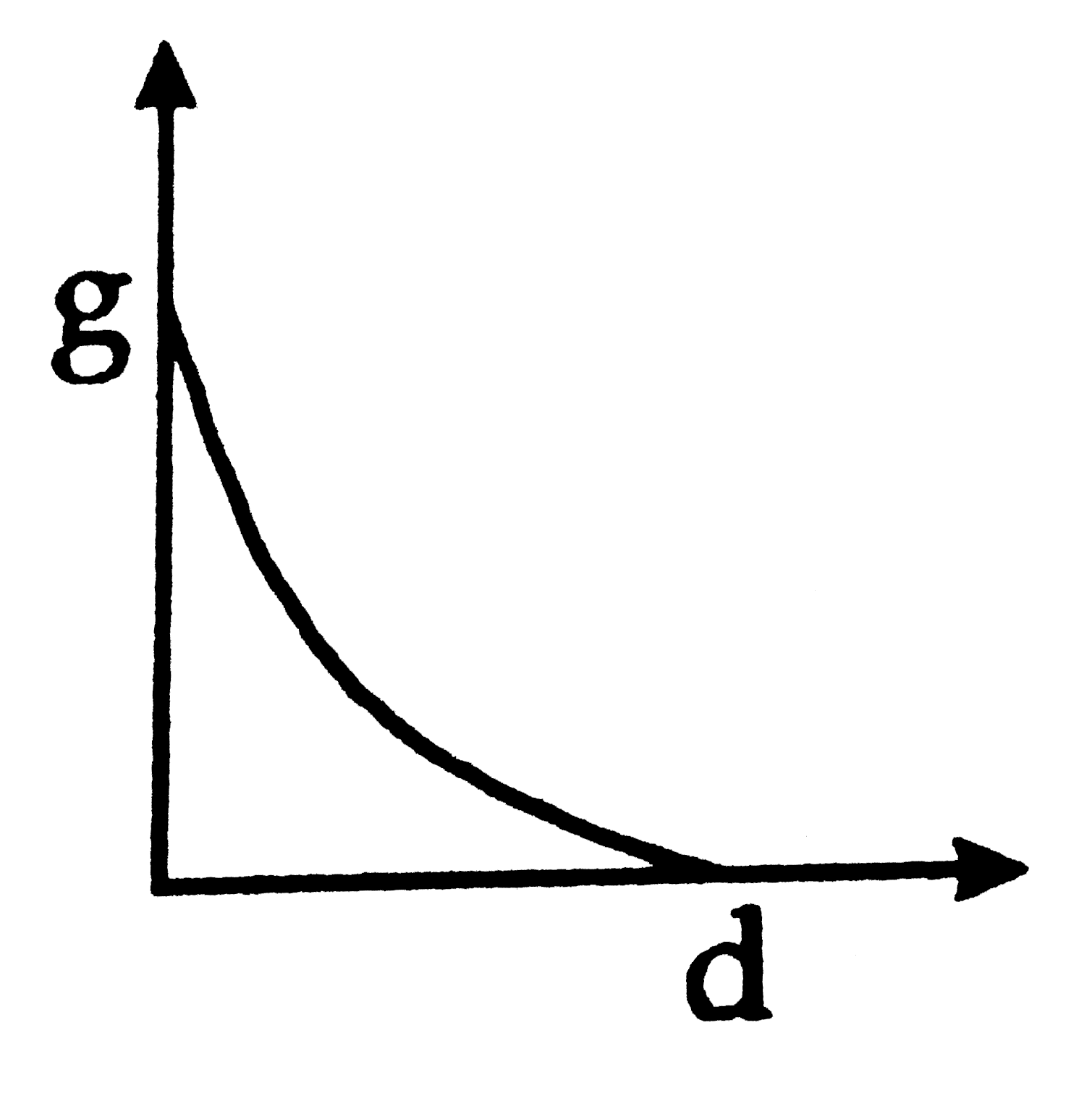
Play - Derive an expression for the variation of g with the height from the s...
04:37
|
Playing Now - What is a geostationary statellite? What are the basic requirements fo...
03:27
|
Play - Define escape velocity of an object.
04:55
|
Play - State Kepler's laws of planetary motion.
07:59
|
Play - Knowing the value of g, how can we calculated the mass and density of...
02:04
|
Play