A dipole of dipole moment p is placed at...

A dipole of dipole moment p is placed at origin along x axis. Another dipole of dipole moment also p is kept at (0, 1, 0) along y axis. Find the resultant potential and electric field at (1, 0, 0).

Text Solution

Verified by Experts

We have studied that the electric field and potential both obey the law of superposition. We can find the electric field and the potential due to each of the dipole at the point concerned and then add them. The caution to be exercised is that while finding the electric field/potential due to a given dipole, we need to consider the center of that dipole as the origin.
Calculation: Due to the first dipole at the origin, the potential is
`V_1 = (kp cos theta)/( r^2) = ( kp)/(1^2) = kp`
Due to the second dipole at y = 1, the potential is
`V_(2) = (kp cos theta)/( r^2) = ( kp) /( sqrt(2)^2) cos 135^(@) = (kp)/( 2 sqrt2)`
Therefore,
`V= V_(1) + V_(2) = kp- (kp sqrt2)/( 4)" "`. (Answer)
Similarly, the electric field in the radial direction due to the first dipole is
`E_(r 1) = ( 2k p cos 0)/( r^3) overset(^) (i) = 2k p overset(^)(i)`.
Here, the radial direction is also the x direction as can be seen from Fig. 24-35.
`E_(p1) = ( 2k p sin 0)/( r^3) overset(^) (j) = 0 overset(^)(j)`.

Here, the polar direction is the positive y direction.
The magnitude of the electric field in the radial direction due to the second dipole is
`- cos 45 overset(^) (i) - sin 45 overset(^)(j) E_(r2) = ( 2k p) /( 2 sqrt2) cos 135^(@) = - (kp)/(2).`
Here, the radial direction is shown in Fig. 24-36. A unit vector in the radial direction will be cos `45overset(^)(i) - sin 45 overset(^)(j)`. So,
`E_(r2) =- (kp)/(2) ((overset(^)(i))/(sqrt2) - (overset(^)(j))/(sqrt2)).`
Similarly, the electric field in the polar direction will be given by
`overset(to) (E_(p2))= (kp sin 135^(@) )/( ( sqrt2)^(3)) (- (overset(^)(i) )/( sqrt2)- (overset(^)(j))/(sqrt2))`.

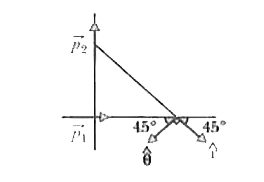
Because a unit vector in polar direction will be `- cos 45 overset(^)(i) - sin 45 overset(^)(j)`, so we have
`overset(to)(E) = 2kp overset(^)(i) - (kp)/( 2 sqrt2) overset(^)(i) + (kp)/( 2 sqrt2) overset(^)(j) - (kp)/(4 sqrt2) overset(^)(j) - (kp)/(4 sqrt2) overset(^)(i) - (kp)/( 4 sqrt2) overset(^)(j)`
`=((kp (8 sqrt2 - 3 )overset(^)(i) )/(4 sqrt2) + (kp overset(^)(j) )/(4 sqrt2) )." "` (Answer)

Topper's Solved these Questions

ELECTRIC POTENTIAL
RESNICK AND HALLIDAY|Exercise SAMPLE PROBLEM 24.20 Dipole moment of combination of three charges|1 Videos
ELECTRIC POTENTIAL
RESNICK AND HALLIDAY|Exercise SAMPLE PROBLEM 24.21 Potential energy of a system of three charged particles|1 Videos
ELECTRIC POTENTIAL
RESNICK AND HALLIDAY|Exercise SAMPLE PROBLEM 24.18 Electric field due to a dipole at a point on dipole axis|1 Videos
ELECTRIC CHARGES AND FIELDS
RESNICK AND HALLIDAY|Exercise Practice Questions (Integer Type )|3 Videos
ELECTROMAGNETIC INDUCTION
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS (Integer Type)|14 Videos

Two short dipoles, each of diple moment p , are placed at origin. The dipole moment of one dipole is along x-axis, while that of other is along y-axis . The electric field at a point (a,0) is given by

`((1)/( 4pi epsilon_(0))) (2p)/(a^(3))`

`((1)/( 4pi epsilon_(0))) (p)/(a^(3))`

`((1)/( 4pi epsilon_(0))) (sqrt(5)p)/(a^(3))`

Zero

An electric dipole of dipole moment p is placed in a uniform external electric field E. Then, the

toeque experienced by the dipole is `E xxp`

torque is zero, if p is perpendicular to E

torque is maximum, if p is perpendicular to E

potential energy is maximum, if p is parallel to E

A dipole of dipole moment P is kept at the centre of a ring of radius R and charge Q the dipole moment has direction along the ring due to the dipole is :

zero

`(kpQ)/(R^(3))`

`(2kpQ)/(R^(3))`

`(kpQ)/(R^(3))` only if the change is uniformly distributed on the ring .