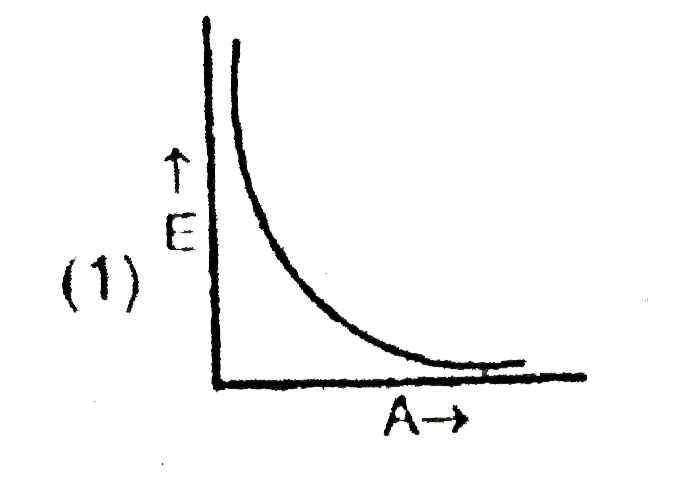
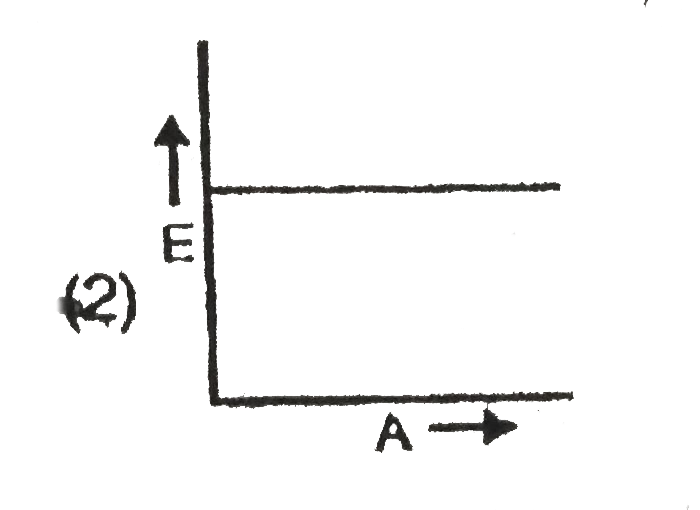
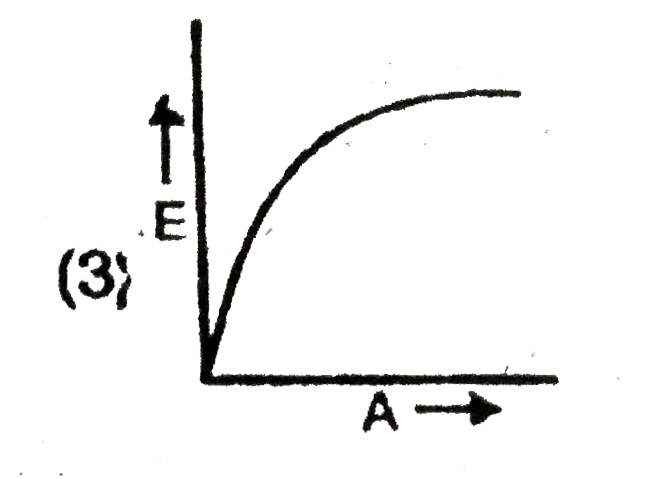
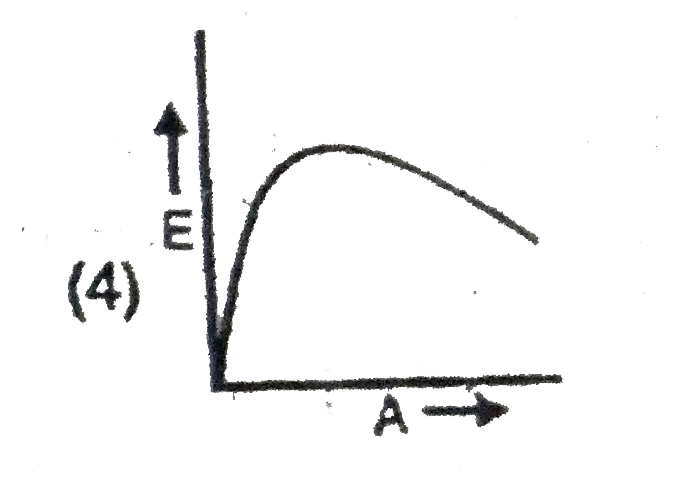
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
NUCLEAR CHEMISTRY
ERRORLESS |Exercise Ordinary Thinking (Rate of decay and Half - life)|97 VideosView PlaylistNUCLEAR CHEMISTRY
ERRORLESS |Exercise Ordinary Thinking (Artificial transmutation )|59 VideosView PlaylistNUCLEAR CHEMISTRY
ERRORLESS |Exercise JEE SECTION (Matrix Match Type Questions)|2 VideosView PlaylistNITROGEN CONTAINING COMPOUNDS
ERRORLESS |Exercise JEE (ADVANCED) 2018 MORE THAN ONE CHOICE CORRECT ANSWER|1 VideosView PlaylistORES, MINERALS AND METALLURGICAL EXTRACTION
ERRORLESS |Exercise JEE ANSWER TPYE QUESTION (JEE Advanced) 2018) Numeric answer type question|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
ERRORLESS -NUCLEAR CHEMISTRY -Ordinary Thinking (Causes of radioactivity and Group displacement law)
- The number of alpha and beta-particles emitted during the transformati...
02:46
|
Play - During the transformation of .^(b)X(a) rarr .^(d)Y(c) the number of be...
Text Solution
|
Play - The mass of helium atom is 4.0026 amu, while that of the neutron and p...
03:11
|
Playing Now - .(72)^(108)X overset(2 alpha)rarr overset(beta)rarr overset(gamma)rarr...
Text Solution
|
Play - The number of neutrons in the parent nucleus which gives N^14 on beta-...
04:36
|
Play - When a radioactive element emits an electron the daughter element form...
02:40
|
Play - The disintegration of an isotope of sodium .(11)Na^(24) rarr .(12)Mg^(...
02:11
|
Play - If a noble gas emits one alpha-particle then it will be shifted in gro...
01:11
|
Play - Ac89^231 gives Pb82^207 after emission of some alpha and beta-partic...
03:48
|
Play - Which element is the end product of each natural radioactive series
01:26
|
Play - Which of the following does not take place by alpha-decay
01:53
|
Play - Which one of the following is not correct
02:18
|
Play - Which one of the following notations shows the product incorrectly ?
01:54
|
Play - .(95)Am^(241) and .(90)Th^(234) belongs respectively to
Text Solution
|
Play - The end product of (4n +1) radioactive disintegration series is
Text Solution
|
Play - In the following nuclear reactions .(7)N^(14) + .(2)He^(4) rarr .(8)...
02:34
|
Play - What is the symbol for the nucleus remaining after .(20)Ca^(42) underg...
01:31
|
Play - beta-particle is emitted in radioactivity by
01:43
|
Play - The radioactive series whose end product is .(83)^(209)Bi is
02:45
|
Play - Radioactive disintegration differs from a chemical change inbeing a)An...
01:33
|
Play