A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
PARABOLA
IIT JEE PREVIOUS YEAR|Exercise TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (INTEGER )|1 VideosView PlaylistPARABOLA
IIT JEE PREVIOUS YEAR|Exercise TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (ANALYTICAL & DESCRIPTIVE )|4 VideosView PlaylistPARABOLA
IIT JEE PREVIOUS YEAR|Exercise TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS I (MATCH THE COLUMNS )|1 VideosView PlaylistMISCELLANEOUS
IIT JEE PREVIOUS YEAR|Exercise MISCELLANEOUS|87 VideosView PlaylistPERMUTATIONS AND COMBINATIONS
IIT JEE PREVIOUS YEAR|Exercise Dearrangement and Number of Divisors (Fill in the Blank )|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
IIT JEE PREVIOUS YEAR-PARABOLA-TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (ONE OR MORE THAN ONE CORRECT OPTION )
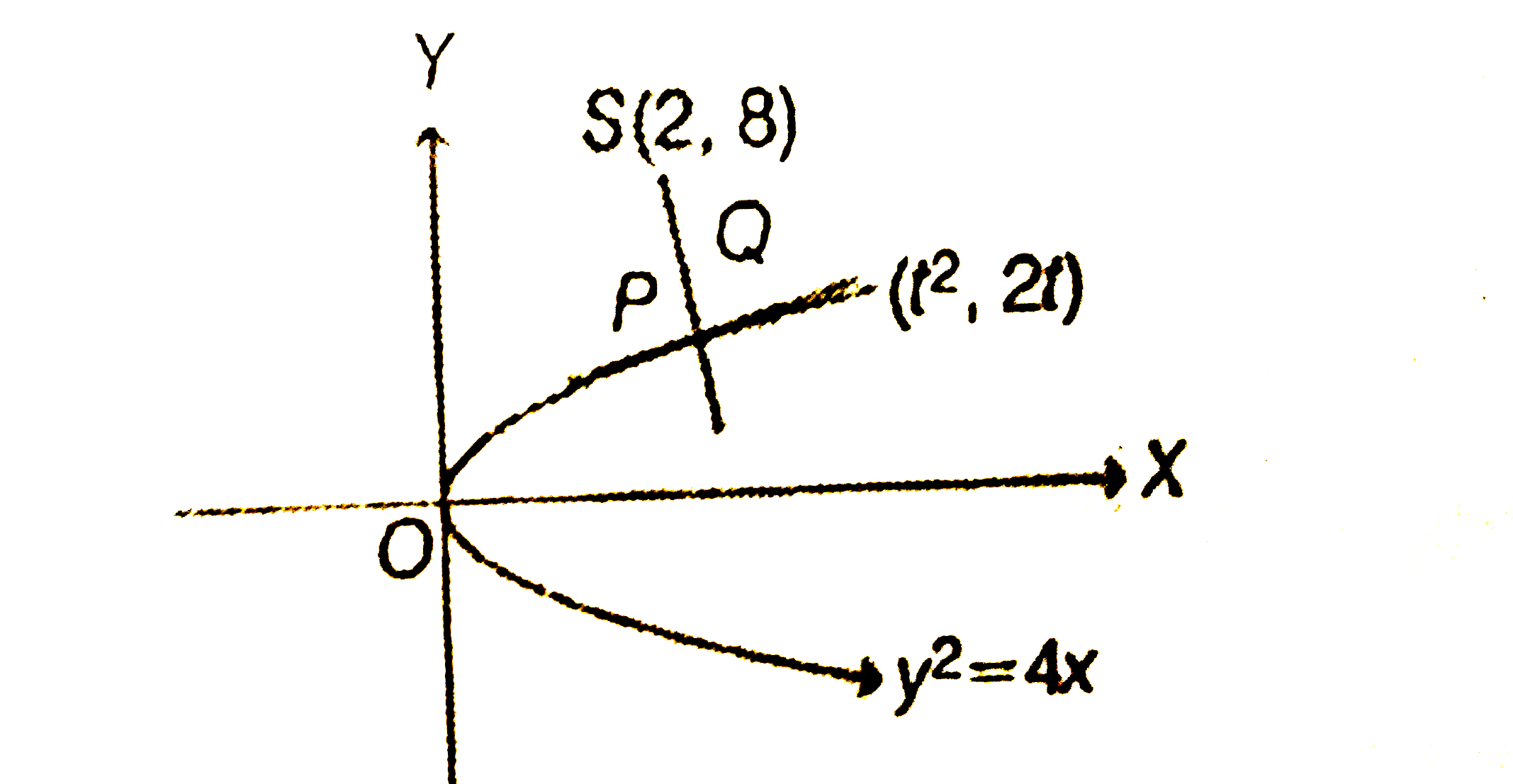
- Let P be the point on parabola y^2=4x which is at the shortest distanc...
05:14
|
Playing Now - A solution curve of the differential equation (x^2+xy+4x+2y+4)((dy)/(d...
10:32
|
Play - Let L be a normal to the parabola y^2=4x.If L passes through the point...
02:29
|
Play - The tangent PT and the normal PN to the parabola y^2=4ax at a point P...
03:39
|
Play