Home
Class 12
MATHS
·If the normals of the parabola y^2=4x...

·If the normals of the parabola `y^2=4x` drawn at the end points of its latus rectum are tangents to the circle `(x-3)^2 (y+2)^2=r^2` , then the value of `r^2` is

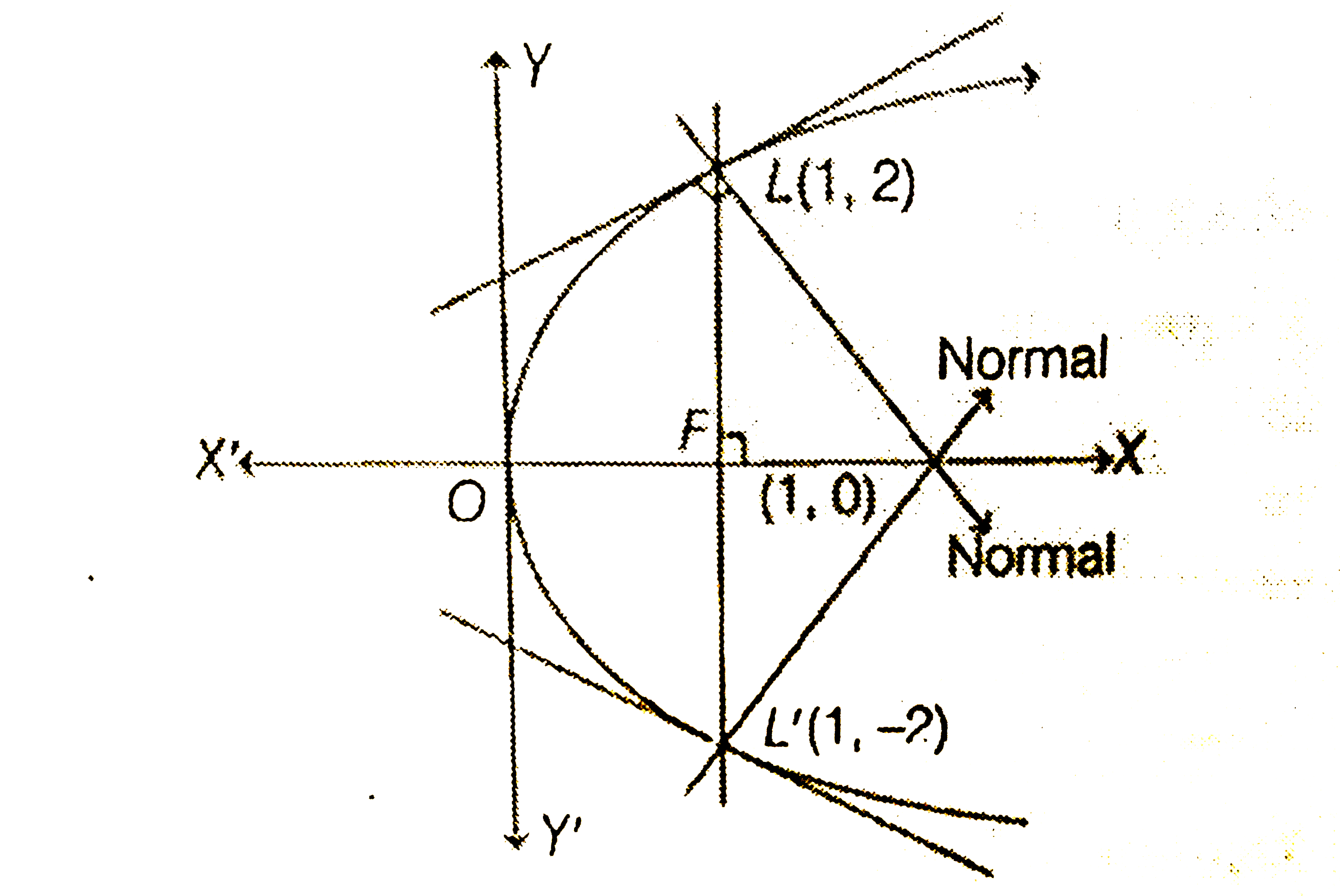
Text Solution

Verified by Experts

The correct Answer is:
2
End points of latusrectum are `(a +- 2a)` i.e. `(1 +- 2)`
Equation of normal at `(x_(1), y_(1))` is
`(y - y_(1))/(x - x_(1)) = (y_(1))/(2a)`
i.e., `(y - 2)/(x - 1) = - (2)/(2)` and `(y + 2)/(x - 1) = (2)/(3)`
`implies x + y + 3`
and `x - y = 3`
Which is tangent to `(X - 3)^(2) + (y + 2)^(2) = r^(2)`

`:.` Length of perpendicular from centre = Radius
`implies (|3 - 2 - 3|)/(sqrt(1^(2) + 1^(2))) = r`
`:. r^(2) = 2`
Promotional Banner

Topper's Solved these Questions

  • PARABOLA

    IIT JEE PREVIOUS YEAR|Exercise TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (ANALYTICAL & DESCRIPTIVE )|4 Videos

  • PARABOLA

    IIT JEE PREVIOUS YEAR|Exercise TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ONE OR MORE THAN ONE CORRECT OPTION )|4 Videos

  • PARABOLA

    IIT JEE PREVIOUS YEAR|Exercise TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (ONE OR MORE THAN ONE CORRECT OPTION )|4 Videos

  • MISCELLANEOUS

    IIT JEE PREVIOUS YEAR|Exercise MISCELLANEOUS|87 Videos

  • PERMUTATIONS AND COMBINATIONS

    IIT JEE PREVIOUS YEAR|Exercise Dearrangement and Number of Divisors (Fill in the Blank )|1 Videos

Similar Questions

Explore conceptually related problems

If the normals of the parabola y^(2)=4x drawn at the end points of its latus rectum are tangents to the circle (x-3)^(2)+(y+2)^(2)=r^(2) , then the value of r^(4) is equal to

Find the equations of normal to the parabola y^(2)=4ax at the ends of the latus rectum.

The point of intersection of the normals to the parabola y^(2)=4x at the ends of its latus rectum is

The normal to y^(2)=4a(x-a) at the upper end of the latus rectum is

If the line 2x+3y=1 touches the parabola y^(2)=4ax then the length of latus rectum is

The end points of the latus rectum of the parabola x ^(2) + 5y =0 is

The end points of latus rectum of the parabola x ^(2) =4ay are

Slope of tangent to the circle (x-r)^(2)+y^(2)=r^(2) at the point (x.y) lying on the circle is

What is the area of the parabola y^(2) = x bounde by its latus rectum ?

IIT JEE PREVIOUS YEAR-PARABOLA-TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (INTEGER )
  1. ·If the normals of the parabola y^2=4x drawn at the end points of it...

    Text Solution

    |