Text Solution
Verified by Experts
|
Topper's Solved these Questions
XII BOARDS
XII BOARDS PREVIOUS YEAR|Exercise SECTION - D|6 VideosView PlaylistXII BOARDS
XII BOARDS PREVIOUS YEAR|Exercise SECTION - E|6 VideosView PlaylistXII BOARDS
XII BOARDS PREVIOUS YEAR|Exercise [SET -III, OUTSIDE DELHI]|5 VideosView PlaylistSAMPLE PAPER 2019
XII BOARDS PREVIOUS YEAR|Exercise SECTION D|6 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
XII BOARDS PREVIOUS YEAR-XII BOARDS-SECTION - C
- (a) State Biot - Savart law and ecpress it in the vector form. (b...
Text Solution
|
Play - Define electric flux and write its SI unit . The electric field compon...
06:04
|
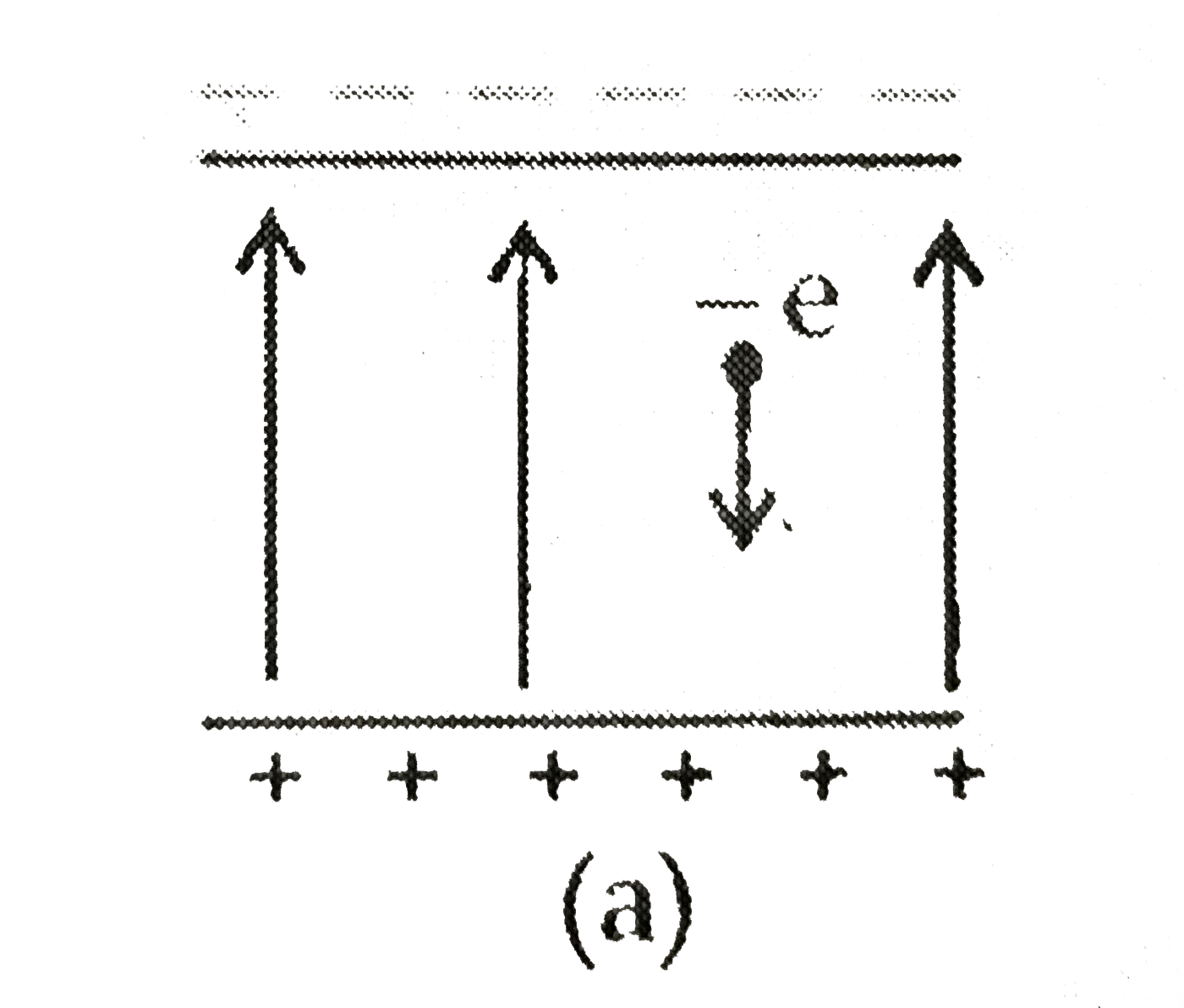
Play - An electron falls through a distance of 1.5 cm in a uniform electric f...
07:06
|
Playing Now - Using Kirchhoff ' s rules , calculate the potential difference between...
Text Solution
|
Play - Define SI unit of current in terms of the force between two parallel c...
16:12
|
Play - (a) With the help pf a ray diagram , show how a concave mirror is use...
Text Solution
|
Play - Two cells of emfs epsilon(1)and epsilon(2) and internal resistances ...
04:56
|
Play - (i) Write two points to distinguish between interference and diffracti...
08:29
|
Play - (a) When an unpolarized light of intensity I(0) is passed through a p...
Text Solution
|
Play - (a) Write the truth table for the combination of the gates shown in th...
04:28
|
Play - When a given photosensitive material is irradiated with light of frequ...
04:46
|
Play - (a) Draw graph showing the variation of current versus voltage in an e...
07:25
|
Play - For the circuit would the balancing length increase, decrease or remai...
07:55
|
Play - State the underlying princeiple of mater bridge. Draw the circuit diag...
Text Solution
|
Play - A proton, a deuteron and an alpha particle, are accelerated through th...
08:23
|
Play - (a) Briefly explain how a galvanometer is converted into an ammeter. ...
02:52
|
Play - (a) Briefly explain how a galvanometer is converted into a voltmeter. ...
03:33
|
Play - The figure shows arectangular conducting frame MNOP of resistance R pl...
04:17
|
Play - Draw aray diagram to show the image formation of a distant object by a...
Text Solution
|
Play - (a) Plot a graph for angle of deviation as a function of angle of inci...
Text Solution
|
Play