(a) Consider an infinitely long straight charged wire of linear charge density `lambda`. To find electric field at a point P situated at a distance r from the wire by using Gauss. law consider a cylinder of length l and radius r as the Gaussian surface.
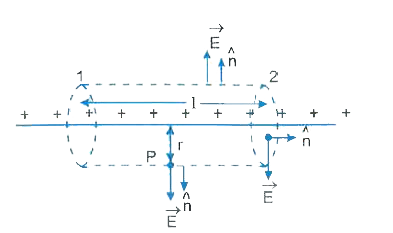
From symmetry consideration electric field at each point of its curved surface is `vecE` and is pointed outwards normally. Therefore, electric flux over the curved surface
`=intvecE.hatn ds=E 2pirl`
On the side faces 1 and 2 of the cylinder normal drawn on the surface is perpendicular to electric field E and hence these surfaces do not contribute towards the total electric flux.
`therefore `Net electric flux over the entire Gaussian surface `phi_(E)=E.2pirl" ....(i)"`
By Gauss law electric flux `phi_(E)=(1)/(in_(0))" (charged enclosed)"=(lambdal)/(in_(0))" ...(ii)"`
Comparing (i) and (ii), we have
`E.2pirl =(lambdal)/(in_(0))`
`rArr" "E=E=(lambda)/(2pi in_(0)r) and vecE=(lambda)/(2pi in_(0)r)hatr`
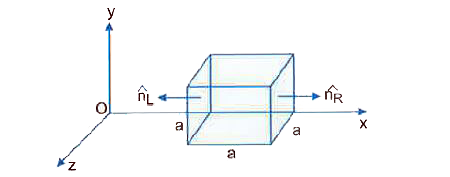
(b) (i) Here, `E_(x)=alpha. x=400x, E_(y)=E_(z)=0 and a=0.1m`. So the electric flux is linked with only two fa c es of the cube lying in Y -Z plane (i.e., perpendicular to `E_(x)`).
As position of left face of cube is at `x=a=0.1m`, hence `(E_(x))_(1)=400xx0.1=40NC^(-1)` (inward into the Cube)
Now position of right face of cube is `x=a+a=2a=0.2m`,
hence `(E_(x))_(2)=400xx0.2=80NC^(-1)`.
`therefore" flux "phi_(2)=(E_(x))_(2).A^(2)=80xx0.01=0.8Nm^(2)C^(-1)" (outward)"`
`therefore` Net flux `phi_(2)=(E_(x))_(2.)A^(2)=80xx0.01=0.8Nm^(2)C^(-1)" (outward)"`
`therefore` Net flux through the cube `phi_(E)=phi_(2)-phi_(1)=0.8-0.4=0.4Nm^(2)C^(-1)` outward
(ii) Charge within the cube `q=in_(0).phi_(E)=(8.854xx10^(-12))xx0.4=3.54xx10^(-12)C`