(a) A current carrying solenoid behaves like a small bar magnet field of solenoid is similar to that of a bar magnet. Magnet field lines inside a current carrying solenoid are parallel straight lines along its axis . Outside the solenoid, is cut into two pieces then we get two smaller solenoids with weaker magnetic properties just like a bar magnet. Consider a solenoid of length .2l. and radius .a. `(a lt lt 2l)` and having .n. turns per unit length . Let us calculate magnetic field B at a point P on its axis situated at a distance .r. form the centre `O(r gt l)` For this purpose , we consider a circular element of solenoid coil situated at a distance x from centre and of thinness .dx. so that it contains .ndx. number of turns.
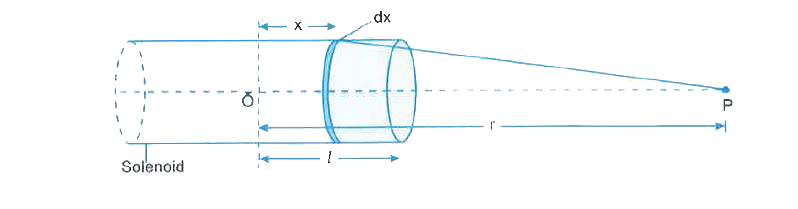
This element may be considered a small circular coil and magnetic field due to it at point P will be
`dB=(mu_0(ndxI)a^2)/(2[(r-x)^2+a^2]^(3//2))`
However , as `a lt lt l` (and hence `a lt lt r ` also) , the above relation may be simplified as :
`dB=(mu_0(ndxI)a^2)/(2(r-x)^3)`
`:.` Magnitude of total magnetic field at P due to entire solenoid.
`B = intdB=int_(-l)^(+l)(mu_0nIa^2dx)/(2(r-x)^3)=(mu_0nIa^2)/2.[(1)/(2(r-x)^2)]_(-l)^(+l)`
`=(mu_0)/(4pi).(4pia^(2)nIrl)/((r^(2)-l^2))=(mu_0)/(4pi).(2(nIpia^(2)2l)r)/((r^2-l^2)^2)`
`=(mu_0)/(4pi).(2mr)/((r^2-l^2)^2)`, where `nIpia^(2).2l=m=` magnetic dipole moment of solenoid coil.
If `r gt gt l`, then we have
`B=(mu_0)/(4pi) .(2m)/r^3`
(b) Here current I = 2 A, no of turns in the coil N = 5 and radius a = 7 cm = 0.07 cm
`:.` Magnetic dipole moment m NIA `NIpia^2=5xx2xx(22)/7xx(0.07)^2=0.308Am^(2)=0.31A m^2`
Since coil lies in X - Y plane, the magnetic dipole moment is along Z - axis i.e., `vecm=0.31 hatk Am^2`
