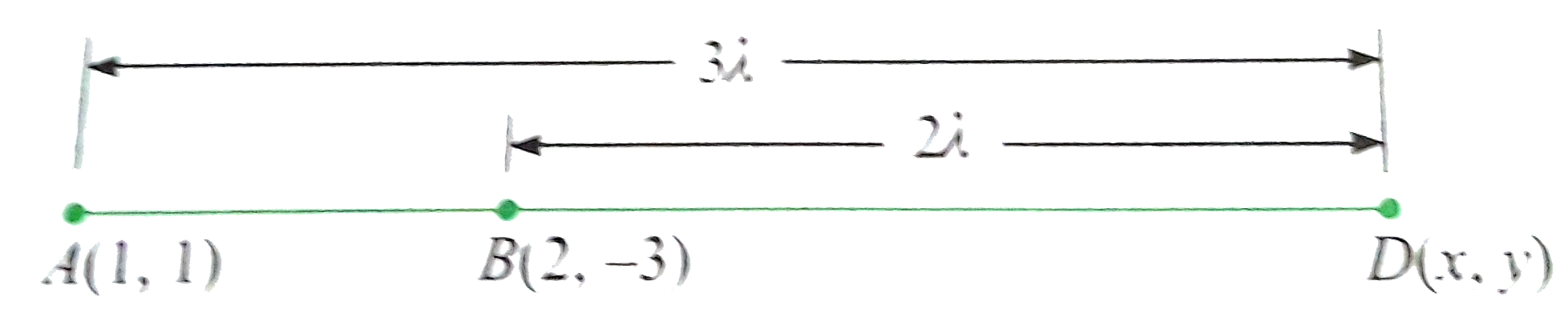Home
Class 12
MATHS
A(1, 1) and B(2,-3) are two points and D...

A(1, 1) and B(2,-3) are two points and D is a point on AB produced such that AD = 3AB. Find the co-ordinates of D.

Text Solution

Verified by Experts

We have `(AD)/(AB)=3`
`therefore(AD)/(AD-AB)=(3)/(3-1)`
`rArr(AD)/(BD)=(3)/(2)`

`therefore (x,y)-=((3(2)-2(1))/(3-2),(3(-3)-2(1))/(3-2))-=(4,-11)`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • COORDINATE SYSYEM

    CENGAGE ENGLISH|Exercise Illustration1.25|1 Videos

  • COORDINATE SYSYEM

    CENGAGE ENGLISH|Exercise Illustration1.26|1 Videos

  • COORDINATE SYSYEM

    CENGAGE ENGLISH|Exercise Illustration1.23|1 Videos

  • COORDINATE SYSTEM

    CENGAGE ENGLISH|Exercise Multiple Correct Answers Type|2 Videos

  • CROSS PRODUCTS

    CENGAGE ENGLISH|Exercise DPP 2.2|13 Videos

Similar Questions

Explore conceptually related problems

Given that A(1,1) and B(2,-3) are two points and D is a point on A B produced such that A D=3A Bdot Find the coordinates of Ddot

Let A(2,-1,4) and B(0,2,-3) be the points and C be a point on AB produced such that 2AC=3AB , then the coordinates of C are

A(1, 4) and B (4, 8) are two points. P is a point on AB such that AP=AB+BP . If AP=10 , find the coordinates of P .

If D(3,-2) , E(-3,1) and F(4,-3) are the mid-points of the sides BC, CA and AB respectively of Delta ABC , find the co-ordinates of point A , B and C .

A straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find : the co-ordinates of points C and D.

The line joining the points A (-3, -10) and B (-2, 6) is divided by the point P such that (PB)/(AB) = (1)/(5). Find the co-ordinates of P.

A straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find : the co-ordinates of point M.

A is a point on x- axis, and point B (5,-4) and AB = 5 units find the co-ordinates of A.

If veca & vecb are the position vectors of A & B respectively and C is a point on AB produced such that AC=3AB then the position vector of C is:

A(20, 0) and B (10, -20) are two fixed points. Find the co-ordinates of the point P in AB such that : 3PB = AB. Also , find the co-ordinates of some other Point Q in AB such that : AB = 6 AQ.

Home
Profile