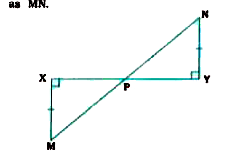
In the given figure, XM and YN are both `lt` perpendicular to line segment XY and XM = YN. 4 Prove that P is the midpoint of XY as well as MN

In the given figure, AB and DC are both perpendicular to line segment AD. BC intersects AD at P and P is the midpoint of AD. Prove that, ( 1 ) AB = CD ( 2 ) P is the midpoint of BC.

AD and BC are equal perpendiculars to a line segment AB (see the given figure) Show that CD bisects AB.

In the given figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that.

In the given figure, lines XY and MN intersect at O. If anglePOY=90^(@) and a:b=2:3 , find c.

In the given figure, the line segment XY is parallel to side AC of DeltaABC and it divides the Deltainto two parts of equal areas. Find the ratio (AX)/(AB) .

Consider two points P and Q with position vectors 2vec(a)+vec(b) and vec(a)-3vec(b) respectively. Find the position vector of a point R which divide the line segment joining P and Q in the ratio. 1 : 2 externally. Prove that P is a midpoint of line segment RQ.

The point A(2,7) lies on the perpendicular bisector of the line segment joining the points P(6,5) and Q(0,-4).

In the given figure bar(PQ) is a line. Ray bar(OR) is perpendicular to line bar(PQ) . bar(OS) is another ray lying between rays bar(OP) and bar(OR) . Prove that angleROS = (1)/(2) angleQOS − anglePOS

Two particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide : (i) The velocity of M is (Mv)/((M + 2m)) (ii) The speed of each of the other particles is ((sqrt2M (M + m))/((M + 2m)))v .